-
Главная
-
Полезные советы
-
Критерий Стьюдента
Критерий Стьюдента
Важным этапом перед практическим использованием построенной модели регрессии является проверка гипотезы о значимости коэффициентов модели парной регрессии. Значимость коэффициентов означает их значимое отличие от нуля.
Выдвинутые гипотезы проверяются с помощью t-критерия (t-статистики) Стьюдента. При этом наблюдаемое значение t-критерия
t набл сравнивают со значением t-критерия, определенным по таблице распределения Стьюдента (с критическим значением)
tтабл .
Критическое значением t-критерия tтабл (a; n-k) зависит от уровня значимости и числа степеней свободы.
Уровень значимости aопределяется как
a = 1 - g, где величина g - доверительная вероятность попадания оцениваемого параметра в доверительный интервал. Доверительную вероятность необходимо брать близкую к единице (0,99; 0,95). Число степеней свободы определяется как разность между объемом выборки (
n) и числом оцениваемых параметров по данной выборке (
k). Для модели парной линейной регрессии число степеней свободы равно (
n-2), т.к. по выборке оцениваются только 2 параметра (
a0 и
a1).
Наблюдаемое значение t-критерия Стьюдента для проверки гипотезы о незначимости коэффициентов модели регрессии:
, где
a1' - оценка коэффициента модели регрессии
a1,
w (a1) - величина стандартной ошибки коэффициента модели регрессии
a1.
Если модуль наблюдаемого значения
t-критерия больше критического значения
t-критерия |
t набл| >
t табл , то с вероятностью (
1 - a) основная гипотеза о незначимости коэффициентов модели регрессии отвергается (коэффициенты модели регрессии значимо отличаются от нуля). Если модуль наблюдаемого значения
t-критерия меньше или равен критическому значению
t-критерия | t набл | ≤
t табл ,то с вероятностью
a основная гипотеза о незначимости коэффициентов модели регрессии принимается (коэффициенты модели регрессии почти не отличаются от нуля или равны нулю).
Если испытываете трудности в написании
курсовой работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
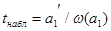, где a1' - оценка коэффициента модели регрессии a1, w (a1) - величина стандартной ошибки коэффициента модели регрессии a1.
Если модуль наблюдаемого значения t-критерия больше критического значения t-критерия | t набл| > t табл , то с вероятностью (1 - a) основная гипотеза о незначимости коэффициентов модели регрессии отвергается (коэффициенты модели регрессии значимо отличаются от нуля). Если модуль наблюдаемого значения t-критерия меньше или равен критическому значению t-критерия | t набл | ≤ t табл ,то с вероятностью a основная гипотеза о незначимости коэффициентов модели регрессии принимается (коэффициенты модели регрессии почти не отличаются от нуля или равны нулю).
Если испытываете трудности в написании курсовой работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.