-
Главная
-
Полезные советы
-
Центральное растяжение - сжатие
Центральное растяжение - сжатие
Из кинематики деформаций следует, что каждое продольное волокно работает на растяжение – сжатие как отдельный стержень и поперечные силы, приходящиеся на сечение волокна с как угодно малой площадью равны нулю. Следовательно, средние касательные напряжения в этом сечении и в сечениях остальных продольных волокон равны нулю. Это возможно, если касательные напряжения во всех точках каждого нормального к оси бруса сечения равны нулю, т.е.
τ
xy= τ
xz= 0 (4.13)
Так как в каждом сечении все продольные волокна испытывают одинаковые деформации (4.4), то в силу (4.11а) нормальные напряжения в каждом поперечном сечении так же будут одинаковы и равны средним
σ
x= N / A (4.14)
Факт отсутствия в поперечных сечениях бруса касательных напряжений не означает их отсутствия при растяжении – сжатии вообще (просто сечения нормальные к оси являются главными площадками – см. раздел 2.3 ). В плоскости, наклонённой на угол α к оси бруса, действуют полные, нормальные и касательные напряжения, которые нетрудно найти из условия равновесия элемента бруса ограниченного указанными сечениями (рис.4.5):
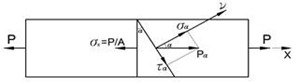
Рис. 4.5 Чистое растяжение – сжатие, элемент бруса с наклонной гранью и напряжения на ней..
р
α = σ
x cos α;
σ
α = σ
x cos
2 α; (4.15)
τ
α = 0.5 σ
x sin2α.
τ
max = σ
x / 2 при α = 45
о (4.16)
Экстремальные касательные напряжения (4.16) являются основной причиной разрушения пластичных материалов, а сами пластические деформации сопровождаются интенсивными сдвигами по направлению τ
max и визуально наблюдаются на поверхности отполированных образцов (линии Чернова – Людерса – Гартмана).
Из (4.4) следует
du= ε
x dx
Интегрируя обе части от а до x, найдём
u = u(a) +
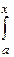
ε
x dx (4.17)
или с учётом (4.11б)
u = u(a) +
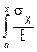
dx (4.18)
В частности, при Е = const
u = u(a) +
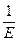
![clip_image004[1] clip_image004[1]](https://moscow-stud.com/wp-content/uploads/e84c864692df_F1C8/clip_image0041_thumb.gif)
σ
x dx (4.19)
Если в интервале a<x<b N= const и A= const, то обозначив l= b - a с учётом (4.14) получим
u = u(a) +
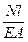
(4.20)
и Δl =
![clip_image010[1] clip_image010[1]](https://moscow-stud.com/wp-content/uploads/e84c864692df_F1C8/clip_image0101_thumb.gif)
, (4.21)
где Δl – абсолютная деформация участка бруса длиной l.
Произведение EA носит название жесткость бруса на растяжение.
Полученные выше зависимости следует дополнить условием прочности (4.6,4.7) выраженным через напряжения
σ ≤ [σ] , (4.22)
где [σ] = σ
пред / n (4.23)
- т.н. допускаемые напряжения, n-коэффициент запаса тот же, что и в (4.7).
Если испытываете трудности в написании
курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
 Рис. 4.5 Чистое растяжение – сжатие, элемент бруса с наклонной гранью и напряжения на ней..
рα = σ x cos α;
σα = σ x cos2 α; (4.15)
τα = 0.5 σ x sin2α.
τmax = σ x / 2 при α = 45о (4.16)
Экстремальные касательные напряжения (4.16) являются основной причиной разрушения пластичных материалов, а сами пластические деформации сопровождаются интенсивными сдвигами по направлению τmax и визуально наблюдаются на поверхности отполированных образцов (линии Чернова – Людерса – Гартмана).
Из (4.4) следует
du= ε x dx
Интегрируя обе части от а до x, найдём
u = u(a) +
Рис. 4.5 Чистое растяжение – сжатие, элемент бруса с наклонной гранью и напряжения на ней..
рα = σ x cos α;
σα = σ x cos2 α; (4.15)
τα = 0.5 σ x sin2α.
τmax = σ x / 2 при α = 45о (4.16)
Экстремальные касательные напряжения (4.16) являются основной причиной разрушения пластичных материалов, а сами пластические деформации сопровождаются интенсивными сдвигами по направлению τmax и визуально наблюдаются на поверхности отполированных образцов (линии Чернова – Людерса – Гартмана).
Из (4.4) следует
du= ε x dx
Интегрируя обе части от а до x, найдём
u = u(a) + 