-
Главная
-
Полезные советы
-
Частные случаи движения точки.
Частные случаи движения точки.
Прямолинейное движение точки.
Так как траекторией точки является прямая линия, то
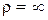
. Тогда
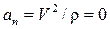
и
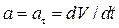
.
Касательное ускорение характеризует изменение скорости по величине.
Равномерное криволинейное движение точки.
При этом движении величина скорости точки остается постоянной
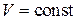
, поэтому
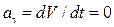
, и
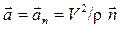
, т. е. вектор ускорения точки
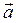
направлен по главной нормали. Нормальное ускорение точки характеризует изменение ее скорости по направлению.
Определим закон равномерного криволинейного движения точки, если при
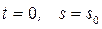
. Так как
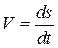
, то
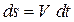
, тогда
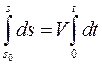
,
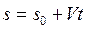
. (1.18)
Формула (1.18) определяет закон равномерного движения точки.
Равнопеременное криволинейное движение точки.
При этом движении
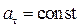
. Определим скорость точки и закон ее движения по известной кривой. Пусть при
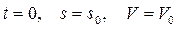
.
Поскольку
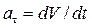
, то
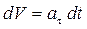
;
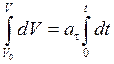
.
Следовательно,
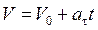
или
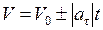
, (1.19)
где знак «+» соответствует равноускоренному движению, а знак «-» - равно-замедленному движению точки.
С учетом (1.12), выражение (1.19) запишем в виде
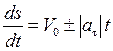
.
Отсюда
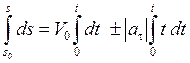
,
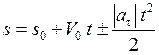
. (1.20)
Формула (1.20) определяет закон равнопеременного криволинейного движения точки.
Равномерное прямолинейное движение точки.
В этом случае вектор скорости не изменяется ни по величине, ни по направлению:
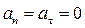
и
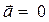
. Таким образом, единственным движением, при котором ускорение точки равно нулю, является равномерное прямолинейное движение.
Определим касательное и нормальное ускорения точки и значение радиуса кривизны ее траектории, если движение точки задано в координатной форме (1.3):
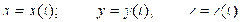
.
Из (1.8) имеем
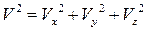
.
Вычислим производную по времени от данного равенства:
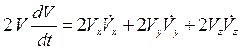
,
отсюда
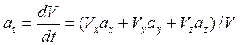
. (1.21)
Из (1.16) находим нормальное ускорение точки
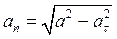
. (1.22)
Тогда значение радиуса кривизны траектории в точке М определим по формуле
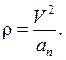
(1.23)
Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
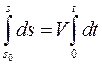 ,
, 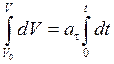 .
Следовательно,
.
Следовательно, 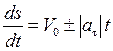 .
Отсюда
.
Отсюда 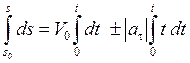 ,
, 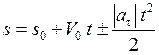 . (1.20)
Формула (1.20) определяет закон равнопеременного криволинейного движения точки.
. (1.20)
Формула (1.20) определяет закон равнопеременного криволинейного движения точки.
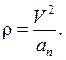 (1.23)
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
(1.23)
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
