-
Главная
-
Полезные советы
-
Дифференциальное уравнение упругой линии балки.
Дифференциальное уравнение упругой линии балки.
Рассмотрим дифференциальное уравнение консольной балки, загруженной парой сил на свободном конце (рис.6.23).

EI
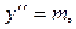
EI
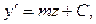
EI
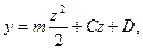
Из граничных условий при z = 0 следует:
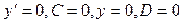
,
EI
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0024_thumb.gif)
Полученное уравнение прогибов представляет квадратичную параболу, но по выражению
![clip_image002[7] clip_image002[7]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0027_thumb.gif)
=
![clip_image004[5] clip_image004[5]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0045_thumb.gif)
= const балка должна изогнуться по дуге окружности. В полученных результатах наглядно проявляется приближенный характер уравнения
![clip_image006[5] clip_image006[5]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0065_thumb.gif)
. Однако, в пределах длины балки ℓ указанные дуги параболы и окружности практически совпадают.
Если балка имеет несколько участков с различными аналитическими выражениями изгибающих моментов, то дифференциальные уравнения упругой линии также будут различны. Интегрирование таких уравнений для
n участков приводит к 2
n постоянных интегрирования. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота сечений на стыке смежных участков. Рассмотрим это на примере балки с двумя участками (рис.6.24).
I участок: 0
![clip_image002[9] clip_image002[9]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0029_thumb.gif)
: EI
x![clip_image004[7] clip_image004[7]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0047_thumb.gif)
=
![clip_image006[7] clip_image006[7]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0067_thumb.gif)
z,
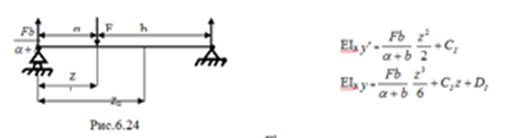
I I участок: α
![clip_image002[11] clip_image002[11]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image00211_thumb.gif)
EI
x![clip_image004[9] clip_image004[9]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0049_thumb.gif)
=
![clip_image006[9] clip_image006[9]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0069_thumb.gif)
z – F(z-α),
EI
x![clip_image008[5] clip_image008[5]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0085_thumb.gif) =
=![clip_image006[10] clip_image006[10]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image00610_thumb.gif)
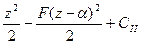
,
EI
x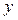 =
=![clip_image006[11] clip_image006[11]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image00611_thumb.gif)
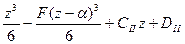
.
Здесь интегрирование идет без раскрытия скобок, т.е., переменной интегрирования является (z – α) а не z, что скажется только на величинах С
I I , D
II
Граничные условия:
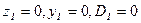
;
![clip_image002[13] clip_image002[13]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image00213_thumb.gif)
,
![clip_image004[11] clip_image004[11]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image00411_thumb.gif)
![clip_image006[15] clip_image006[15]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image00615_thumb.gif)
![clip_image008[7] clip_image008[7]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0087_thumb.gif)
=0,
![clip_image010[4] clip_image010[4]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0104_thumb.gif)
![clip_image012[4] clip_image012[4]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0124_thumb.gif)
![clip_image014[4] clip_image014[4]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0144_thumb.gif)
![clip_image016[4] clip_image016[4]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0164_thumb.gif)
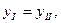
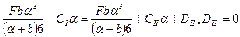
,
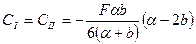 .
.
Если испытываете трудности в написании
контрольной работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
 EI
EI![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/12b5c29691c3_FAD3/clip_image0024_thumb.gif) Полученное уравнение прогибов представляет квадратичную параболу, но по выражению
Полученное уравнение прогибов представляет квадратичную параболу, но по выражению  I I участок: α
I I участок: α 