-
Главная
-
Полезные советы
-
Движение центра масс в динамике.
Движение центра масс в динамике.
Теорема о движении центра масс системы.
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил
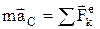
– дифференциальное уравнение движения центра масс. В проекциях на оси координат:
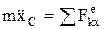
.
Закон сохранения движения центра масс.
Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Аналогично в проекциях на оси, если
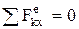
, следовательно
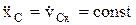
, если при этом в начальный момент v
Cx0= 0, то следовательно
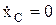
, следовательно x
C= const.
Количество движения системы Q (иногда обозначают К) – вектор, равный геометрической сумме (главному вектору) количеств движения всех точек системы:
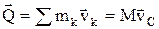
, М – масса всей системы, v
C – скорость центра масс.
Теорема об изменении количества движения системы:
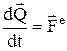
– производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях:
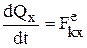
, и т.д. Теорема об изменении кол-ва движения системы в интегральной форме:
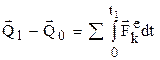
, где
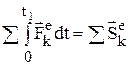
– импульсы внешних сил.
В проекциях: Q
1x – Q
0x = åS
ekx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
Закон сохранения количества движения.
Согласно закону сохранения количества движения, если сумма всех внешних сил, действующих на систему, = 0, то вектор количества движения системы будет постоянен по модулю и направлению:
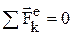
Þ
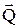
= const, аналогично в проекциях:
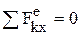
Þ Q
x= const. Из закона следует, что внутренние силы изменить суммарное количество движение системы не могут.
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
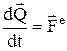 – производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях:
– производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях: 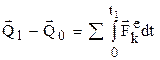 , где
, где 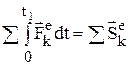 – импульсы внешних сил.
В проекциях: Q1x – Q0x = åSekx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
– импульсы внешних сил.
В проекциях: Q1x – Q0x = åSekx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
