-
Главная
-
Полезные советы
-
Способы задания движения точки.
Способы задания движения точки.
Для задания движения точки применяется один из следующих способов: векторный, координатный или естественный.
Векторный способ
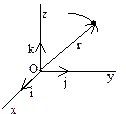
Положение точки определяется ее радиус-вектором
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/e815fa55f3ac_C458/clip_image0024_thumb.gif)
, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, называется годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между координатным и векторным способами:
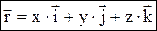
,
(
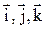
– это орты – единичные вектора, сонаправленные с какой-либо осью)
модуль
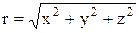
, направляющие косинусы:
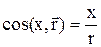
и т.д.
Переход от координатного способа к естественному:
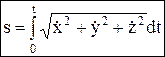
.
Координатный способ
Положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f
1(t), y=f
2(t), z=f
3(t).
Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоскости).
Естественный способ
Указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).
Для задания движения точки естественным способом необходимо:
1) знать траекторию движения точки;
2) выбрать на траектории начало отсчета «О»;
3) установить положительное и отрицательное направление отсчета криволинейной координаты
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/e815fa55f3ac_C458/clip_image0026_thumb.gif)
ОМ;
4) задать закон изменения криволинейной координаты s как функции времени:
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/e815fa55f3ac_C458/clip_image0044_thumb.gif)
.
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
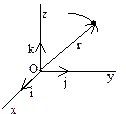 Положение точки определяется ее радиус-вектором
Положение точки определяется ее радиус-вектором 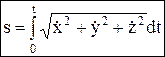 .
.
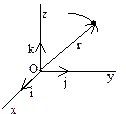 Положение точки определяется ее радиус-вектором
Положение точки определяется ее радиус-вектором 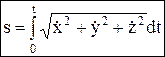 .
.