1. Главная
2. Полезные советы
3. Эпюры поперечных сил и изгибающих моментов.

Эпюры поперечных сил и изгибающих моментов.

Дифференциальные зависимости при изгибе между q, Q, M

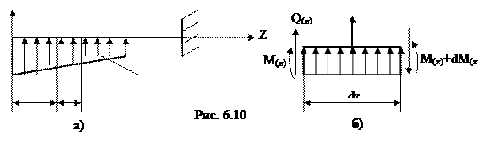
Вырежем из балки на участке с распределенной нагрузкой (рис.6.10 а) элемент длиной dz, по торцам которого будут действовать внутренние усилия (рис.6.10 б). В силу малости участка dz интенсивность распределенной нагрузки на нем можно принять постоянной, тогда её равнодействующая будет равняться q·dz. 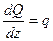Рассмотрим равновесие этого элемента ∑У = 0, Q_(z) + q·dz –Q_(z) - dQ_(z) =0, из этого уравнения следует, что , т.е., производная от поперечной силы Q по длине балки z равна интенсивности распределенной нагрузки q. 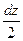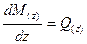В качестве второго уравнения равновесия рассмотрим сумму моментов всех сил относительно правого торца: - M_(z) - Q_(z)·dz - q·dz·+ M_(z) + dM_(z) =0, так как q·dz· величина второго порядка малости, то ею можно пренебречь, тогда , т.е., производная от изгибающего момента по длине балки z равна поперечной силе Q_(z). Полученные соотношения выведены при направлении оси Z слева направо (в правой системе координат). При противоположном её направлении правые части полученных дифференциальных зависимостей изменят знак: ,. 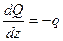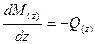Рассмотренные дифференциальные зависимости используются для контроля эпюр Q и М 1. Если на участке балки Q>0, то момент на этом участке возрастает, если Q<0, то момент убывает, если Q=0, то М= const. 2. Если эпюра Q плавно меняет знак (рис. 6.11), то момент в этом сечении принимает экстремальное значение. При смене знака с плюса на минус он будет максимальным, при смене знака с минуса на плюс - минимальным. 3. В сечении балки, где имеется сосредоточенная сила, на эпюре Q будет скачок, равный по величине этой силе, а на эпюре М излом (рис.6.12). 4. В сечении балки, где имеется сосредоточенный момент, на эпюре моментов будет скачок, равный по величине этому моменту (рис.6.13). 5. На участке с распределенной нагрузкой эпюра моментов описывается параболой с выпуклостью на встречу нагрузке (рис.6.14). 6. Эпюры изгибающих моментов, согласно принятым правилам знаков, всегда строятся на сжатых волокнах. 6. Эпюры изгибающих моментов, согласно принятым правилам знаков, всегда строятся на сжатых волокнах.

Напряжения при изгибе

Рассечём балку плоскостью а-а и в её левой части выделим элементарную площадку dА, на которой будут действовать нормальные и касательные напряжения. Рассечём балку плоскостью а-а и в её левой части выделим элементарную площадку dА, на которой будут действовать нормальные и касательные напряжения. Равнодействущая элементарных усилий σdА будет равняться изгибающему моменту М, а равнодействующая τdА будет равна поперечной силе Q. Таким образом, нормальные напряжения в балке зависят только от момента, а касательные от силы Q (рис.6.15) Если испытываете трудности в написании контрольной работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.