-
Главная
-
Полезные советы
-
Физический маятник в динамике.
Физический маятник в динамике.
Физический маятник – твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси под действием силы тяжести. Уравнение вращательного движения:

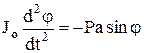
, обозначая
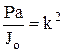
, получаем дифференциальное уравнение колебаний маятника:
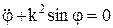
, k – частота колебаний маятника. Рассматривая малые колебания, можно считать sinj » j, тогда
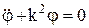
– дифференциальное уравнение гармонических колебаний. Решение этого уравнения: j = С
1coskt + C
2 sinkt или j = asin(kt + b), a – амплитуда колебаний маятника, b – начальная фаза колебаний. Период малых колебаний физического маятника Т= 2p/k = 2p
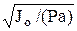
. Для малых колебаний маятника период не зависит от угла начального отклонения, этот результат является приближенным.
Для математического маятника (материальной точки, подвешенной на нерастяжимой нити и движущейся под действием силы тяжести) имеем дифференциальные уравнения движения:
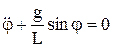
, L – длина нити. Если L=
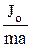
, то математический маятник будет двигаться так же, как и физический (период колебаний совпадает). Величина L называется приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии ОК=L, называется центром качаний физического маятника. Если ось подвеса взять в точке К, то точка О будет центром качаний и наоборот – свойство взаимности. Расстояние ОК всегда >ОС, т.е. центр качаний всегда расположен ниже центра масс.
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.

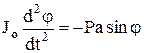 , обозначая
, обозначая 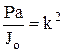 , получаем дифференциальное уравнение колебаний маятника:
, получаем дифференциальное уравнение колебаний маятника: 