-
Главная
-
Полезные советы
-
Формула Эйлера для критической силы.
Формула Эйлера для критической силы.
Вывод формулы Эйлера рассмотрим на примере опорной балки, нагруженной сжимающей осевой силой F. При F=F
кр балка прогнется. Запишем дифференциальное уравнение изогнутой оси:
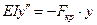
,
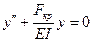
.
здесь I=I
min.
y
w + k
2y = 0 (8.1).
Обозначим
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/192a8bc92385_D1CB/clip_image0024_thumb.gif)
, получим дифференциальное уравнение второго порядка без правой части.
Его решение имеет вид:
![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/192a8bc92385_D1CB/clip_image00210_thumb.gif)
.
Значения А и В определятся из граничных условий (z = 0 и z=ℓ). В рассматриваемой балке имеем при z=0 y=0; при z=ℓ y=0. Тогда из
(8.1) следует
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/192a8bc92385_D1CB/clip_image0044_thumb.gif)
так как
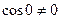
, sinkℓ≠0, то В=0, тогда Asinkℓ=0.
Но A≠0, так как балка не будет иметь прогибов, поэтому sinkℓ=0, т.е. kℓ=0,
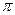
, 2π, 3π,…nπ.
Из последнего равенства находим k
2=
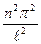
=
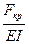
,
откуда следует формула
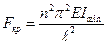
,
n≠0, тогда при n=1 получим окончательное выражение для критической силы, называемой формулой Эйлера:
![clip_image002[12] clip_image002[12]](https://moscow-stud.com/wp-content/uploads/192a8bc92385_D1CB/clip_image00212_thumb.gif)
(8.2)
Если испытываете трудности в написании
курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
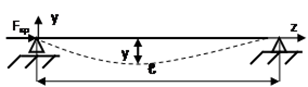
![clip_image002[12] clip_image002[12]](https://moscow-stud.com/wp-content/uploads/192a8bc92385_D1CB/clip_image00212_thumb.gif) (8.2)
Если испытываете трудности в написании курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
(8.2)
Если испытываете трудности в написании курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
