1. Главная
2. Полезные советы
3. Группировка статистических данных и анализ групп

Группировка статистических данных и анализ групп

Группировкой называется выделение единиц исследуемой совокупности на однородные группы по определенным, существенным для них признакам. Устойчивое разграничение объектов выражается классификацией, которая основывается на самых существенных признаках (например, классификация отраслей народного хозяйства, классификация основных фондов и т.д.). Таким образом, классификация – это узаконенная, общепринятая, нормативная группировка. Принято различать следующие виды группировок: типологическая, структурная, аналитическая. Типологическая группировка - это разделение качественно неоднородной совокупности на отдельные качественно однородные группы и выявление на этой основе типовых признаков. Структурная группировка — это выявление закономерностей распределения единиц однородной совокупности по варьирующим значениям исследуемого признака. Структурные группировки отличаются от типологических не столько по внешнему виду, сколько по целям, т. е. отличаются по уровню качественных различий между группами. Аналитическая группировка — это исследование взаимосвязей варьирующих признаков в пределах однородной совокупности. При ее построении можно установить взаимосвязи между двумя признаками и более. При этом один признак будет группировочным или факторным (условно независимым), а другой (другие) — результативным (ми). Аналитические группировки — применяются для выявления взаимосвязи, взаимозависимости и взаимодействия изучаемых явлений. Основные этапы построения аналитической группировки следующие: · обоснование и выбор факторного и результативного признаков; · группировка единиц совокупности по факторному признаку; · подсчет числа единиц в каждой из образованных групп, а также определение объема варьирующих признаков в пределах созданных групп; · исчисление средних размеров результативного показателя (признака) по каждой из образованных групп; · оформление результатов группировки в таблице; · сопоставление изменения значений факторного и результативного признаков, определяющее характер связи между ними, т. е. выявление взаимосвязи между признаками, когда с возрастанием значения факторного признака систематически возрастает или убывает значение признака результативного. Для установленного числа групп определяются интервалы группировки - значение варьирующего признака, лежащее в границах интервала: нижняя границы (или хотя бы одна из них) это наименьшее значение признака в интервале; верхняя — наибольшее значение признака в интервале. Величина интервала – промежуток между максимальными и минимальными значениями признака в группе (т.е. разность между верхней и нижней границами интервала). Интервалы бывают: · равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова; · неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе; · закрытые, когда имеются и нижняя, и верхняя границы, например, заработная плата сотрудников определяется в тыс. руб.: 1 - 5; 5 – 10; 10 - 15; 15 – 20; 20 – 30;. · открытые, когда имеется только либо верхняя, либо нижняя граница, например, заработная плата сотрудников определяется в тыс. руб.: до 3; 3 – 15; 15 – 30; 30 и более. Интервалы группировки в зависимости от однородности (варьируемости) группировочного признака могут быть равные и неравные. 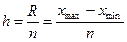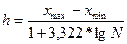Если вариация признака проявляется в сравнительно узких границах и ее распределение носит равномерный характер, то группировка проводится с равными интервалами, величина которого определяется: или где — x_maxи x_min — максимальное и минимальное значения признака в совокупности; n — число групп. Если максимальное и минимальное значения (x_max- x_min – размах вариации) существенно отличаются от других единиц группировочного признака, то для определения величины интервала следует использовать не максимальное и минимальное значения, а значения, несколько превышающие минимум и несколько меньшие, чем максимум. Если размах вариации признака велик и его значения варьируются неравномерно, то необходимо использовать группировку с неравными интервалами. Применение неравных интервалов обусловлено тем, что первых группах небольшая разница в показателях имеет больше значение, а в последних группах эта разница несущественна. В зависимости от величины размаха вариации, неравные интервалы могут быть прогрессивно-возрастающими или прогрессивно-убывающими в арифметической (при сильном разбросе данных) или геометрической прогрессии (разброс данных очень сильный). Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом: h_i+1 = h_i+ a, а в геометрической прогрессии: hi+1 = hi * q, где a — константа, имеющая для прогрессивно-возрастающих интервале знак «+», а для прогрессивно-убывающих интервалов знак «-»; q — константа (для прогрессивно-убывающих интервалов q > 1; в другом случае - q< 1). Например, при анализе заработной платы в группах «разнорабочие», «квалифицированный персонал», «руководители» целесообразно рассматривать неравные интервалы в арифметической прогрессии, а при очень сильной дифференциации – в геометрической.