Главная
Полезные советы
Вычислите коэффициенты корреляции рангов Спирмена и Кендалла Y(X) и Z(X).

Вычислите коэффициенты корреляции рангов Спирмена и Кендалла Y(X) и Z(X).

Имеются исходные статистические данные в таблицах: Таблица 1 Описание набора исходных данных

№ столбца	Переменная	Описание
1	N	Номер элемента выборки
2	X	Значения признака xi
3	Y	Значения признака yi
4	Z	Значения признака zi
5	G	Уровни ряда динамики gt

Таблица 2 Файл данных

N	X	Y	Z	G
1	12	-41	-26	55
2	14	-37	14	54
3	8	-10	11	51
4	24	-72	-62	51
5	3	-10	-20	47
6	7	-19	-25	43
7	8	-20	38	43
8	19	-62	-51	42
9	19	-64	10	50
10	26	-78	-27	62
11	22	-77	-16	73
12	26	-83	-30	70
13	14	-42	31	75
14	26	-86	-90	70
15	5	-14	-23	69
16	13	-28	-46	61
17	8	-36	-88	57
18	27	-75	-86	55
19	12	-36	-40	49
20	12	-31	-64	63
21	25	-76	-48	62
22	17	-56	-10	73
23	12	-40	25	76
24	28	-78	-76	88
25	7	-13	-14	88
26	3	-14	-55	87
27	5	-11	-14	82
28	16	-56	-55	77
29	23	-72	-34	75
30	26	-82	-31	71

Вычислите коэффициенты корреляции рангов Спирмена и Кендалла Y(X) и Z(X). Сделайте вывод о тесноте связи.

Решение:

Расчеты выполним для коэффициентов корреляции рангов Спирмена и Кендалла Y(X). Коэффициент ранговой корреляции Спирмена между переменными X и Y находится по формуле

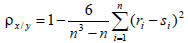
где

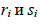
- ранги i-го объекта по переменным X и Y, n − число пар наблюдений. Составим таблицу: Таблица 9

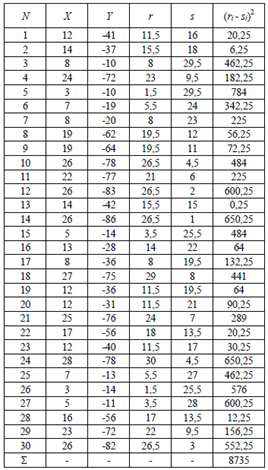
Тогда по формуле (2) имеем:

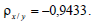
Коэффициент ранговой корреляции Кендалла между переменными X и Y находится по формуле:

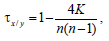
где K – статистика Кендалла, представляющая собой минимальное число обменов между элементами последовательности s, необходимое для приведения ее к упорядочиванию, аналогичному последовательности r. Для определения статистики K необходимо ранжировать объекты по одной переменной (пусть, для определенности по X) в порядке возрастания (при этом ее ранги будут упорядочены ( n r1 ≤ r2 ≤K≤ r ) и определить соответствующие им ранги si, i = 1, … , n, переменной Y. Статистика K равна общему числу инверсий (нарушений порядка, когда большее число стоит слева от меньшего), в ранговой последовательности n s , s , , s 1 2 K . Результаты расчетов приведены в табл. 10. Таблица 10

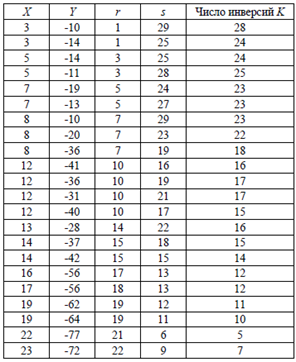
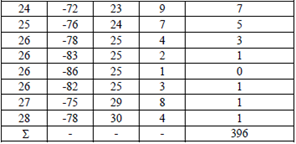
Сумма всех инверсий: K = 396. Теперь по (3)

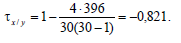
Большие по величине значения ранговых коэффициентов корреляции свидетельствуют о наличии тесной связи между признаками X и Y. Если испытываете трудности в написании контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.

N	X	Y	Z	G
1	12	-41	-26	55
2	14	-37	14	54
3	8	-10	11	51
4	24	-72	-62	51
5	3	-10	-20	47
6	7	-19	-25	43
7	8	-20	38	43
8	19	-62	-51	42
9	19	-64	10	50
10	26	-78	-27	62
11	22	-77	-16	73
12	26	-83	-30	70
13	14	-42	31	75
14	26	-86	-90	70
15	5	-14	-23	69
16	13	-28	-46	61
17	8	-36	-88	57
18	27	-75	-86	55
19	12	-36	-40	49
20	12	-31	-64	63
21	25	-76	-48	62
22	17	-56	-10	73
23	12	-40	25	76
24	28	-78	-76	88
25	7	-13	-14	88
26	3	-14	-55	87
27	5	-11	-14	82
28	16	-56	-55	77
29	23	-72	-34	75
30	26	-82	-31	71

N	X	Y	Z	G
1	12	-41	-26	55
2	14	-37	14	54
3	8	-10	11	51
4	24	-72	-62	51
5	3	-10	-20	47
6	7	-19	-25	43
7	8	-20	38	43
8	19	-62	-51	42
9	19	-64	10	50
10	26	-78	-27	62
11	22	-77	-16	73
12	26	-83	-30	70
13	14	-42	31	75
14	26	-86	-90	70
15	5	-14	-23	69
16	13	-28	-46	61
17	8	-36	-88	57
18	27	-75	-86	55
19	12	-36	-40	49
20	12	-31	-64	63
21	25	-76	-48	62
22	17	-56	-10	73
23	12	-40	25	76
24	28	-78	-76	88
25	7	-13	-14	88
26	3	-14	-55	87
27	5	-11	-14	82
28	16	-56	-55	77
29	23	-72	-34	75
30	26	-82	-31	71

N	X	Y	Z	G
1	12	-41	-26	55
2	14	-37	14	54
3	8	-10	11	51
4	24	-72	-62	51
5	3	-10	-20	47
6	7	-19	-25	43
7	8	-20	38	43
8	19	-62	-51	42
9	19	-64	10	50
10	26	-78	-27	62
11	22	-77	-16	73
12	26	-83	-30	70
13	14	-42	31	75
14	26	-86	-90	70
15	5	-14	-23	69
16	13	-28	-46	61
17	8	-36	-88	57
18	27	-75	-86	55
19	12	-36	-40	49
20	12	-31	-64	63
21	25	-76	-48	62
22	17	-56	-10	73
23	12	-40	25	76
24	28	-78	-76	88
25	7	-13	-14	88
26	3	-14	-55	87
27	5	-11	-14	82
28	16	-56	-55	77
29	23	-72	-34	75
30	26	-82	-31	71