1. Главная
2. Полезные советы
3. Метод наименьших квадратов (МНК)

Метод наименьших квадратов (МНК)

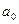
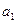
Существуют определенные методы оценки неизвестных параметров и модели парной регрессии:

Метод наименьших квадратов (МНК)

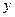
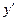
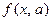
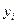
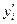
Рассчитывается сумма квадратов отклонений наблюдаемых значений результативной переменной от теоретических значений (рассчитанных на основании функции регрессии ). Согласно методу наименьших квадратов неизвестные параметры и выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений от теоретических значений была минимальной. С учетом этого параметры уравнения регрессии определяются следующим образом: , . 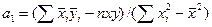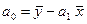Достоинства МНК: сведение всех вычислительных процедур к простому вычислению неизвестных коэффициентов; доступность математических выводов. Недостатки МНК: чувствительность оценок к резким выбросам, встречающимся в исходных данных. Метод наименьших квадратов является наиболее распространенным методом оценки неизвестных параметров модели парной линейной регрессии.

Метод наименьших модулей (МНМ)

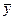
Рассчитывается сумма модулей отклонений наблюдаемых значений результативной переменной от теоретических значений . Согласно этому методу неизвестные параметры и выбираются таким образом, чтобы сумма модулей отклонений эмпирических значений от теоретических значений была минимальной. Достоинства МНМ: нечувствительность оценок к резким выбросам. 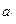Недостатки МНМ: 1) сложность вычислительной процедуры; 2) возможность соответствия различным значениям оцениваемых коэффициентов , одинаковых сумм модулей отклонений. Таким образом, метод наименьших квадратов существенно проще при проведении вычислительной процедуры и дает хорошие по статистическим свойствам оценки. Этим и объясняется его широкое применение в оценивании параметров эконометрических моделей. Если испытываете трудности в написании контрольной работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.