1. Главная
2. Полезные советы
3. Множественная регрессия

Множественная регрессия

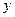
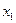
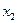
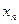
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной от нескольких объясняющих переменных ,,…,. Эта задача решается с помощью множественного регрессионного анализа. Модель множественной линейной регрессии, в которой зависимая переменная, возмущения и объясняющие переменные удовлетворяют приведенным выше предпосылкам регрессионного анализа и, кроме того, предпосылке о невырожденности матрицы (независимости столбцов) значений объясняющей переменной (см. далее) называется классической нормальной линейной моделью множественной регрессии. Предполагается, что объясняющие переменные некоррелированы друг с другом. 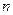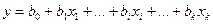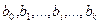На основе наблюдений получают выборочное уравнение множественной линейной ре­грессии: _, где — оценки параметров уравнения множественной регрессии . 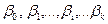Для оценки параметров уравнения множественной регрессии используется метод наимень­ших квадратов (МНК). Любая сумма квадратов связана с числом степеней свободы — с числом независимого варьирования пере­менных. Введение в модель каждого нового параметра уменьшает на 1 число степеней свободы. Необходимым условием минимума суммы квадратов остатков является равенство нулю всех ее частных производных по коэф­фициентам уравнения регрессии . 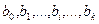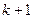Такое условие приходит к системе из () линейного урав­нения с () неизвестным, называемой системой нормальных уравнений. Ее решение обычно записывается в матричной форме. 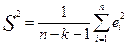Стандартной ошибкой регрессии, несмещенной оценкой дисперсии модели является величина S² (остаточная дисперсия): Если условия Гаусса-Маркова, определяющие воз­можность применения МНК, выполняются, то оценки параметров множественной регрессии являются несмещенными, состоятель­ными и эффективными. Пусть в уравнении регрессии содержится k объясняющих переменных. 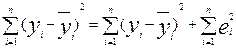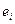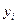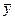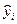Дисперсию зависимой переменной можно разло­жить на объясненную и необъясненную составляющие: где — остаток в i-м варианте реализации событий; — значение зависимой переменной в i-м варианте реали­зации событий; — среднее значение зависимой переменной; — расчетное значение зависимой переменной в i-м вари­анте реализации событий, определяемое уравнением регрессии; — число вариантов реализации событий, в каждом из ко­торых при сочетании значений независимых переменных было получено значение зависимой переменной. 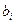Значимость коэффициентов уравнения регрессии оце­нивается с помощью t-критерия. Порядок оценки по критерию Стьюдента следующий. Вычисляется наблюдаемое зна­чение критерия . 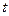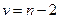По таблице распределения Стьюдента по задан­ному уровню значимости и числу степеней свободы находят критическое значение . 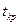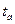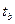Вычисленные критерии и сравниваются с критическим значением . 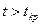Если , то соответствующий коэффициент уравнения ре­грессии значим и принимается. 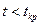Если , то соответствующий коэффициент уравнения регрессии незначим, не отличается от нуля и не принимается. В эконометрике проверку гипотез осуществляют при 5%-м, реже на 10%-м уровне значимости. В первом случае стандартная ошибка коэффициента регрессии составляет примерно до половины его величины. Последовательный отсев несущественных факторов — переменных, коэффициенты при которых оказались незначимы, составляет основу многошагового регрессионного анализа. 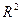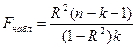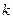Для определения статисти­ческой значимости коэффициента детерминации использу­ется F-статистика, рассчитываемая по формуле: , где — число пар данных в выборке, использованных для полу­чения уравнения регрессии; — количество коэффициентов в уравнении регрессии. 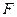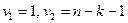Величина имеет распределение Фишера c степенями свободы. 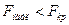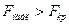Вычисленный критерий сравнивается с кри­тическим значением следующим образом: если , то считается незначимым, он не отличим от нуля; если , то считается значимым, и уравнение регрес­сии может использоваться для объяснения изменения переменной под влиянием изменения переменных . 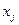Величины критических значений критериев оценки значимости принимаются при 5%-м, реже 10%-м уровне значимости. Указан­ные уровни значимости соответствуют 95%-му и 90%-му довери­тельным интервалам соответственно. Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. При наличии мультиколлинеарности оценки, полученные методом наименьших квадратов (МНК), формально существуют, но обладают рядом недостатков: 1) небольшое изменение исходных данных приводит к суще­ственному изменению оценок регрессии; 2) оценки имеют большие стандартные ошибки, малую значи­мость, в то время как модель в целом является значимой (высо­кое значение коэффициента детерминации). Если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяснить, нет ли среди них сильно коррелированных между собой. При наличии корреляции один из пары связанных между собой факторов исключается. Если статистически незначим лишь один фактор, то он должен быть исключен или заменен другим показателем. В модель регрессии включаются те факторы, которые более сильно связаны с зависи­мой переменной, но слабо связаны с другими факторами. Построение эконометрической модели включает выбор объясняющих переменных — составление их спецификации. Свойства оценок коэффициентов регрессии в значительной мере зависят от правильной спецификации модели. Предположим, что переменная y зависит от двух переменных. Однако в модель включили только одну незави­симую переменную : _. 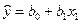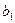В этом случае не включения в модель переменной, которая должна быть включена, оценка и ее дисперсия являются смещенны­ми. 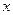Смещенность оценки связана с тем, что если не учесть вторую переменную в регрессии, то переменная , будет играть двой­ную роль: отражать свое прямое влияние и заменять переменную в описании ее влияния. Коэффициент детерминации для данной регрессии отра­жает общую объясняющую способность переменной х₁ в обеих ролях и является завышенной оценкой. При включении в модель переменной, которая не должна быть включена, оценки коэффициентов регрессии и их дисперсии в этом случае являются несмещенными, но неэффек­тивными. Практически обнаруживается, что коэффициенты при излишних переменных статистически незначимы, и эти перемен­ные исключаются из модели. При исследовании влияния качественных признаков в модель следует вводить фиктивные переменные, принимающие, как правило, два значения: 1, если данный признак присутствует в наблюдении; 0 — при его отсутствии. Если испытываете трудности в написании курсовой работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.