-
Главная
-
Полезные советы
-
Моменты инерции в динамике.
Моменты инерции в динамике.
Момент инерции материальной точки относительно некоторой оси называется произведение массы m этой точки на квадрат ее расстояния h до оси: mh
2.
Момент инерции тела (системы) относительно оси Оz: J
z= åm
kh
k2. При непрерывном распределении масс (тело) сумма переходит в интеграл: J
x= ò(y
2+z
2)dm; J
y= ò(z
2+x
2)dm; J
z= ò(x
2+y
2)dm – относительно координатных осей. J
z= M×r
2, r – радиус инерции тела – расстояние от оси до точки в которой нужно сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции тела. Момент инерции относительно оси (осевой момент инерции) всегда >0. Полярный момент инерции J
o= ò( x
2+y
2+z
2)dm; J
x+J
y+J
z= 2J
o.
Центробежный момент инерции
Центробежный момент инерции J
xy для материальной точки называется произведение ее координат x и y на ее массу m. Для тела центробежными моментами инерции называются величины, определяемые равенствами: J
xy=òxy dm; J
yz=òyz dm; J
zx=òzx dm. Центробежные моменты инерции симметричны относительно своих индексов, т.е. J
xy=J
yx и т.д. В отличие от осевых, центробежные моменты инерции могут иметь любой знак и обращаться в нуль. Главной осью инерции тела называется ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. Например, если J
xz=J
yz=0, то ось z – главная ось инерции.
Главной центральной осью инерции называется главная ось инерции, проходящая через центр масс тела.
1) Если тело имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела для точки, в которой ось пересекает плоскость.
2) Если тело имеет ось симметрии, то эта ось является главной осью инерции тела (ось динамической симметрии). Размерность всех моментов инерции [кгм
2]
Центробежный момент инерции зависят не только от направления координатных осей, но и от выбора начала координат.
Тензор инерции в данной точке:
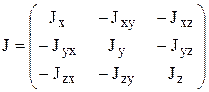
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0024_thumb.gif)
Моменты инерции некоторых однородных тел:
стержень массы m и длины L:

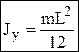
;
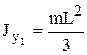
.
Однородный сплошной диск с центром в точке С радиуса R и массы m:
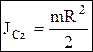
. Полый цилиндр:
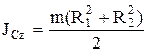
,
цилиндр с массой распределенной по ободу (обруч):
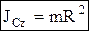
.
Теорема Штейнера
По теореме Гюйгенса-Штейнера момент инерции тела относительно произвольной оси равен моменту инерции относительно оси ей параллельной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями:
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0044_thumb.gif)
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0026_thumb.gif)
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0064_thumb.gif)
Наименьший момент инерции будет относительно той оси, которая проходит через центр масс. Момент инерции относительно произвольной оси L: J = J
xcos
2a + J
ycos
2b + J
zcos
2g – 2J
xycosacosb – 2J
yzcosbcosg – 2J
zxcosgcosa,
если координатные оси являются главными относительно своего начала, то:
J = J
xcos
2a + J
ycos
2b + J
zcos
2g.
Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
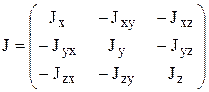
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0024_thumb.gif) Моменты инерции некоторых однородных тел:
стержень массы m и длины L:
Моменты инерции некоторых однородных тел:
стержень массы m и длины L: 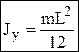 ;
; 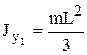 .
Однородный сплошной диск с центром в точке С радиуса R и массы m:
.
Однородный сплошной диск с центром в точке С радиуса R и массы m: 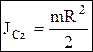 . Полый цилиндр:
. Полый цилиндр: 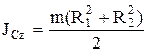 ,
цилиндр с массой распределенной по ободу (обруч):
,
цилиндр с массой распределенной по ободу (обруч): ![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0026_thumb.gif)
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/4cc1a04cbf03_D73B/clip_image0064_thumb.gif) Наименьший момент инерции будет относительно той оси, которая проходит через центр масс. Момент инерции относительно произвольной оси L: J = Jxcos2a + Jycos2b + Jzcos2g – 2Jxycosacosb – 2Jyzcosbcosg – 2Jzxcosgcosa,
если координатные оси являются главными относительно своего начала, то:
J = Jxcos2a + Jycos2b + Jzcos2g.
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
Наименьший момент инерции будет относительно той оси, которая проходит через центр масс. Момент инерции относительно произвольной оси L: J = Jxcos2a + Jycos2b + Jzcos2g – 2Jxycosacosb – 2Jyzcosbcosg – 2Jzxcosgcosa,
если координатные оси являются главными относительно своего начала, то:
J = Jxcos2a + Jycos2b + Jzcos2g.
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
