1. Главная
2. Полезные советы
3. Мультиколлинеарность и методы ее устранения

Мультиколлинеарность и методы ее устранения

Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. Оценка коэффициента уравнения регрессии может оказаться незначимой не только из-за несущественности данного фактора, но и из-за того, что трудно разграничить воздействие на завершающую переменную 2-х или нескольких факторов. Это обычно возникает в том случае, когда факторы линейно связаны между собой и меняются синхронно. Природу мультиколлинеарности наиболее наглядно можно выявить на примере совершенной мультиколлинеарности, то есть в случае, если факторы функционально связаны друг с другом. 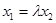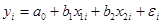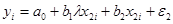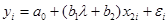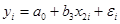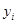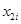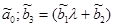Пусть уравнение регрессии имеет вид: (1) (2) Используя соотношение (1) и (2) можем переписать в следующем виде: или Используя и методом наименьших квадратов находим оценки: , но в этом случае имеем одно уравнение с 2-мя неизвестными и следовательно найти значение оценок b₁ и b₂ невозможно. В реальности имеем несовершенную мультиколлинеарность, то есть стахост. линейную связь м/д x₁ и x₂. Оценка этой связи находится путем расчета . 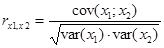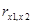Чем ближе к 1, тем ближе несовершенная мультиколлинеарность к совершенной, и тем менее надежными будут оценки коэффициента регрессии при этих переменных. Небольшое смещение ведет к большим изменениям признака. В эконометрических исследованиях считается, что предельным значением коэффициента парной корреляции между двумя факторами должно быть 0,8. Устранение мультиколлинеарности ведется путем исключения одного из факторов из уравнения регрессии. Исключают тот фактор, который:

1. по мнению исследователей считается менее значимым;
2. менее высокий коэф-т (r) с результатом переменной (y);
3. более высокий r с другими факторами

Также можно изменить выборку. Если испытываете трудности в написании курсовой работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.