-
Главная
-
Полезные советы
-
Найдите необходимый объем выборки, с вероятностью 0,99 гарантирующий предельную ошибку оценки среднего веса изделия в партии, равную 0,025 г.
Найдите необходимый объем выборки, с вероятностью 0,99 гарантирующий предельную ошибку оценки среднего веса изделия в партии, равную 0,025 г.
Для установления среднего веса изделия из 300 контейнеров организована серийная выборка с бесповторным отбором. Выбрано 6 контейнеров, каждый из которых содержит 40 изделий. Получены следующие результаты.
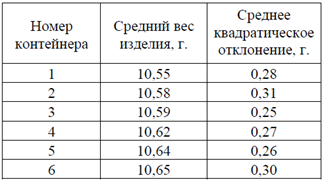
Найдите необходимый объем выборки, с вероятностью 0,99 гарантирующий предельную ошибку оценки среднего веса изделия в партии, равную 0,025 г.
Решение:
Минимально необходимый объем выборки для серийной выборки с бесповторным отбором определяется по формуле
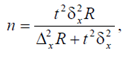
где R – число серий в генеральной совокупности;
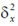
– межсерийная дисперсия; Δx – предельная ошибка веса; t = 2,58 для вероятности 0,99.
По условию известны: R = 300 , Δ = 0,025 x .
Определим межсерийную дисперсию. Она находится по формуле:
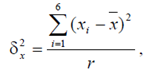
где r – число серий в выборочной совокупности, r = 6 .
Выборочная средняя равна
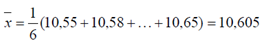
Межсерийная дисперсия равна
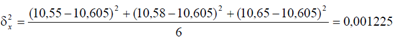
Отсюда имеем
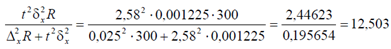
Далее, n ≥ 12,503. Наименьшее число, удовлетворяющее этому условию, = 13 ∗ n .
Таким образом, для того чтобы с вероятностью 0,99 гарантировать предельную ошибку оценки среднего веса изделия в партии 0,025 г., необходимо выбрать не менее 13 контейнеров.
Если испытываете трудности в написании
контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.

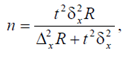 где R – число серий в генеральной совокупности;
где R – число серий в генеральной совокупности; 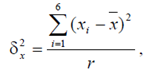 где r – число серий в выборочной совокупности, r = 6 .
Выборочная средняя равна
где r – число серий в выборочной совокупности, r = 6 .
Выборочная средняя равна 