-
Главная
-
Полезные советы
-
Найдите степень корреляции между следующими парами значений x и y.
Найдите степень корреляции между следующими парами значений x и y.
Найдите степень корреляции между следующими парами значений x и y. Определите уравнение регрессии y = a + bx для каждого случая
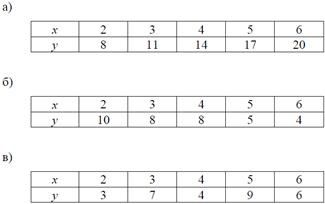
Для каждого из этих случаев с помощью уравнения регрессии определите значение y при x = 7 и прокомментируйте вероятную точность этих прогнозов.
Решение:
Коэффициенты регрессии a, b находим методом наименьших квадратов, решая систему линейных уравнений:
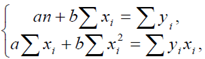
, где n = 5.
Решение данной системы имеет вид:
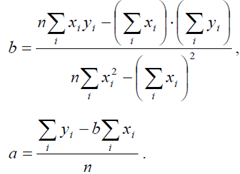
Коэффициент корреляции между x и y равен:
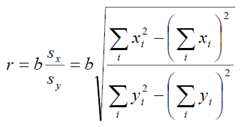
Построим уравнение регрессии y = a + bx для каждого случая.
а) Вспомогательная таблица имеет вид:
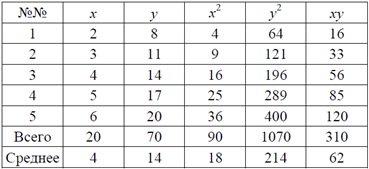
Отсюда, используя приведенные выше формулы, получим
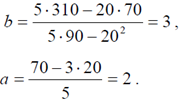
Уравнение регрессии имеет вид: y = 2 + 3x
Коэффициент корреляции между x и y равен:
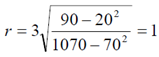
Прогноз среднего значения y при x = 7 равен
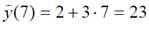
б) Вспомогательная таблица имеет вид:
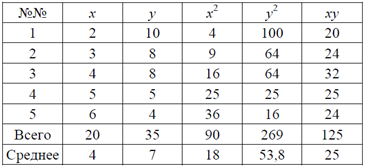
Отсюда, используя приведенные выше формулы, получим:
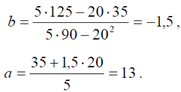
Уравнение регрессии имеет вид: y = 13 – 1,5x
Коэффициент корреляции между x и y равен:
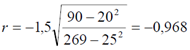
Прогноз среднего значения y при 7 = x равен
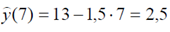
в) Вспомогательная таблица имеет вид:
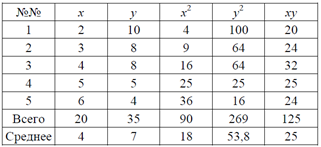
Отсюда, используя приведенные выше формулы, получим:
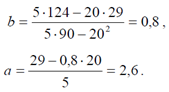
Уравнение регрессии имеет вид: y = 0,8 + 2,6x
Коэффициент корреляции между x и y равен:
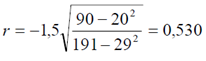
Прогноз среднего значения y при x = 7 равен
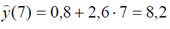
В случае а) имеем линейную функциональную связь. Поэтому точность прогноза здесь 100%-ная. Такие связи в регрессионном анализе не рассматриваются.
В случае б) имеем значимую линейную регрессионную зависимость. В случае в) коэффициент корреляции мал, поэтому связь между величинами статистически не значимая.
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.

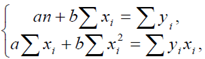 , где n = 5.
Решение данной системы имеет вид:
, где n = 5.
Решение данной системы имеет вид:
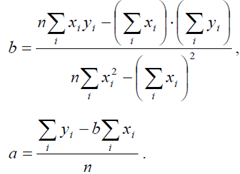 Коэффициент корреляции между x и y равен:
Коэффициент корреляции между x и y равен:
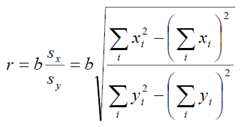 Построим уравнение регрессии y = a + bx для каждого случая.
а) Вспомогательная таблица имеет вид:
Построим уравнение регрессии y = a + bx для каждого случая.
а) Вспомогательная таблица имеет вид:
 Отсюда, используя приведенные выше формулы, получим
Отсюда, используя приведенные выше формулы, получим
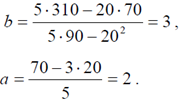 Уравнение регрессии имеет вид: y = 2 + 3x
Коэффициент корреляции между x и y равен:
Уравнение регрессии имеет вид: y = 2 + 3x
Коэффициент корреляции между x и y равен: 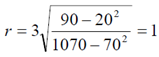 Прогноз среднего значения y при x = 7 равен
Прогноз среднего значения y при x = 7 равен  Отсюда, используя приведенные выше формулы, получим:
Отсюда, используя приведенные выше формулы, получим:
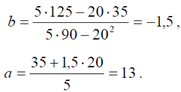 Уравнение регрессии имеет вид: y = 13 – 1,5x
Коэффициент корреляции между x и y равен:
Уравнение регрессии имеет вид: y = 13 – 1,5x
Коэффициент корреляции между x и y равен: 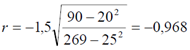 Прогноз среднего значения y при 7 = x равен
Прогноз среднего значения y при 7 = x равен  Отсюда, используя приведенные выше формулы, получим:
Отсюда, используя приведенные выше формулы, получим:
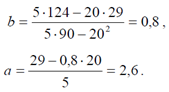 Уравнение регрессии имеет вид: y = 0,8 + 2,6x
Коэффициент корреляции между x и y равен:
Уравнение регрессии имеет вид: y = 0,8 + 2,6x
Коэффициент корреляции между x и y равен: 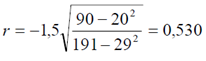 Прогноз среднего значения y при x = 7 равен
Прогноз среднего значения y при x = 7 равен 