-
Главная
-
Полезные советы
-
Найти доверительный интервал для оценки неизвестного математического ожидания а и дисперсии s2.
Найти доверительный интервал для оценки неизвестного математического ожидания а и дисперсии s2.
По выборке объемом п определены выборочное среднее 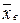 и исправленное среднее квадратическое отклонение s нормально распределенной случайной величины Х. Найти доверительный интервал для оценки неизвестного математического ожидания а и дисперсии s2. Принять Р = 0,95.
и исправленное среднее квадратическое отклонение s нормально распределенной случайной величины Х. Найти доверительный интервал для оценки неизвестного математического ожидания а и дисперсии s2. Принять Р = 0,95.
Решение(1):
Доверительный интервал для оценки неизвестного математического ожидания имеет вид:
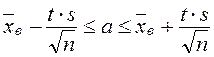
.
По условию задачи величина t распределена по нормальному закону, поэтому ее значение для интегральной функции Лапласа будет составлять
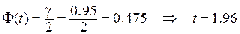
Тогда доверительный интервал имеет вид:

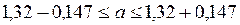
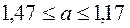
Доверительный интервал для оценки неизвестной дисперсии имеет вид:
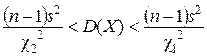
Для величины
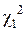
вероятность Р = (1 + 0,95)/2 = 0,975;
Для величины
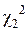
вероятность Р = (1 – 0,95)/2 = 0,025
По числу степеней свободы, равному п–1 = 15, находим из таблицы распределения c2
Находим
![clip_image016[1] clip_image016[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0161_thumb.gif)
= 6,26 и
![clip_image018[1] clip_image018[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0181_thumb.gif)
= 27,5
Тогда искомый доверительный интервал будет иметь вид:
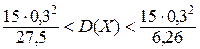
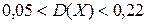
Решение(2):
Доверительный интервал для оценки неизвестного математического ожидания имеет вид:
![clip_image004[1] clip_image004[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0041_thumb.gif)
.
По условию задачи величина t распределена по нормальному закону, поэтому ее значение для интегральной функции Лапласа будет составлять
![clip_image006[1] clip_image006[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0061_thumb.gif)
Тогда доверительный интервал имеет вид:
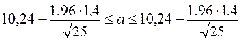
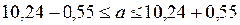
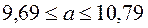
Доверительный интервал для оценки неизвестной дисперсии имеет вид:
![clip_image014[1] clip_image014[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0141_thumb.gif)
Для величины
![clip_image016[2] clip_image016[2]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0162_thumb.gif)
вероятность Р = (1 + 0,95)/2 = 0,975;
Для величины
![clip_image018[2] clip_image018[2]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0182_thumb.gif)
вероятность Р = (1 – 0,95)/2 = 0,025
По числу степеней свободы, равному п–1 = 24, находим из таблицы распределения c2
Находим
![clip_image016[3] clip_image016[3]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0163_thumb.gif)
= 12,4 и
![clip_image018[3] clip_image018[3]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0183_thumb.gif)
= 39,4
Тогда искомый доверительный интервал будет иметь вид:
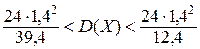
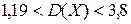
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
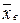 и исправленное среднее квадратическое отклонение s нормально распределенной случайной величины Х. Найти доверительный интервал для оценки неизвестного математического ожидания а и дисперсии s2. Принять Р = 0,95.
и исправленное среднее квадратическое отклонение s нормально распределенной случайной величины Х. Найти доверительный интервал для оценки неизвестного математического ожидания а и дисперсии s2. Принять Р = 0,95.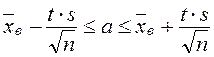 .
По условию задачи величина t распределена по нормальному закону, поэтому ее значение для интегральной функции Лапласа будет составлять
.
По условию задачи величина t распределена по нормальному закону, поэтому ее значение для интегральной функции Лапласа будет составлять
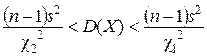 Для величины
Для величины ![clip_image004[1] clip_image004[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0041_thumb.gif) .
По условию задачи величина t распределена по нормальному закону, поэтому ее значение для интегральной функции Лапласа будет составлять
.
По условию задачи величина t распределена по нормальному закону, поэтому ее значение для интегральной функции Лапласа будет составлять
![clip_image014[1] clip_image014[1]](https://moscow-stud.com/wp-content/uploads/s2_AFCC/clip_image0141_thumb.gif) Для величины
Для величины 