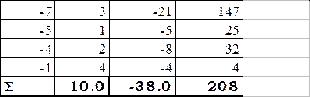-
Главная
-
Полезные советы
-
Найти: а) эмпирическую функцию распределения F*(x); б) точечные оценки параметров распределения.
Найти: а) эмпирическую функцию распределения F*(x); б) точечные оценки параметров распределения.
Задано статистическое распределение выборки. Найти:
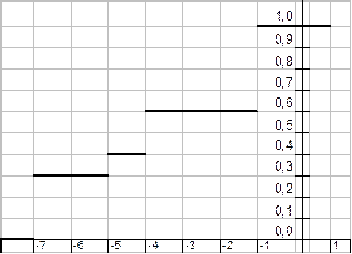
а) эмпирическую функцию распределения F*(x);
б) точечные оценки параметров распределения: выборочное среднее, исправленную дисперсию, исправленное среднеквадратическое отклонение.
| хi |
–7 |
–5 |
–4 |
–1 |
| ni |
3 |
1 |
2 |
4 |
Решение:
а) Эмпирической функцией распределения F*(x) называется относительная частота того, что признак примет значение, меньшее заданного. Другими словами, для данного х эмпирическая функция распределения представляет накопленную частоту F*(x) =
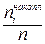
= w
iнакопл
Для эмпирической функции распределения рассчитаем относительные частоты по формуле w
i= n
i /n , где n – объем выборки. Вычисления занесем в таблицу:
| xi |
ni |
wi= ni /n |
F* |
| –7 |
3 |
0,3 |
0,3 |
| –5 |
1 |
0,1 |
0,4 |
| –4 |
2 |
0,2 |
0,6 |
| –1 |
4 |
0,4 |
1,0 |
| S |
n = 10 |
1,0 |
|
Таким образом эмпирическая функция распределения F*(х) имеет вид:
б) Выборочные числовые характеристики вычислим по формулам:
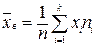
– выборочное среднее;
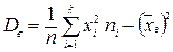
– выборочная дисперсия
Для удобства произведения х
i×n
i и х
2i×n
i вычислим с помощью таблицы:
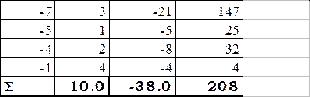
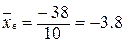
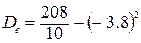
= 20,8 – 14,44 = 6,36
Исправленную дисперсию s
2 найдем по формуле
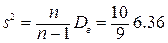
= 7,07
Исправленное среднее квадратическое отклонение s равно квадратному корню из исправленной дисперсии
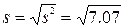
= 2,66
Если испытываете трудности в написании
контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
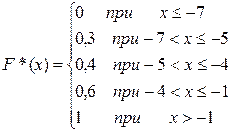
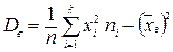 – выборочная дисперсия
Для удобства произведения хi×ni и х2i×ni вычислим с помощью таблицы:
– выборочная дисперсия
Для удобства произведения хi×ni и х2i×ni вычислим с помощью таблицы: