-
Главная
-
Полезные советы
-
Найти вероятность того, что: а) все изделия годные, б) среди выбранных изделий одно бракованное; в) все изделия бракованные.
Найти вероятность того, что: а) все изделия годные, б) среди выбранных изделий одно бракованное; в) все изделия бракованные.
Из партии, в которой 25 изделий, среди которых 6 бракованных, случайным образом выбрали 3 изделия для проверки качества. Найти вероятность того, что: а) все изделия годные, б) среди выбранных изделий одно бракованное; в) все изделия бракованные.
Решение:
а) Пусть событие А состоит в том, что все выбранные изделия годные. Количество возможных способов взять 3 изделия из 25-ти равно
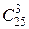
, т.е.
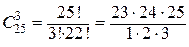
= 2300, а количество возможных способов взять 3 годных изделия из (25 – 6) = 19-ти годных равно
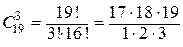
= 1938. Тогда по классическому определению вероятность события А равна
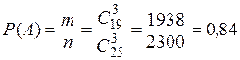
.
б) Пусть событие В состоит в том, что среди выбранных изделий одно бракованное, т.е. одно бракованное и два годных. Количество возможных способов взять 3 изделия из 25-ти равно
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/b77d160fedae_A5A4/clip_image0024_thumb.gif)
= 2300, а количество возможных способов взять одно бракованное изделие из 6-ти бракованных И два годных изделия из (25 – 6) = 19-ти годных равно
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/b77d160fedae_A5A4/clip_image0044_thumb.gif)
*
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/b77d160fedae_A5A4/clip_image0064_thumb.gif)
= 6×153 = 738. Тогда по классическому определению вероятность события В равна
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/b77d160fedae_A5A4/clip_image0084_thumb.gif)
.
в) Пусть событие С состоит в том, что все выбранные изделия бракованные. Количество возможных способов взять 3 изделия из 25-ти равно
![clip_image002[5] clip_image002[5]](https://moscow-stud.com/wp-content/uploads/b77d160fedae_A5A4/clip_image0025_thumb.gif)
= 2300, а количество возможных способов взять 3 бракованные изделия из 6-ти бракованных равно
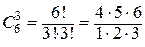
= 20. Тогда по классическому определению вероятность события С равна
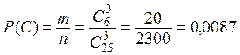
.
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
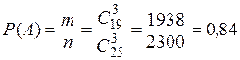 .
б) Пусть событие В состоит в том, что среди выбранных изделий одно бракованное, т.е. одно бракованное и два годных. Количество возможных способов взять 3 изделия из 25-ти равно
.
б) Пусть событие В состоит в том, что среди выбранных изделий одно бракованное, т.е. одно бракованное и два годных. Количество возможных способов взять 3 изделия из 25-ти равно ![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/b77d160fedae_A5A4/clip_image0084_thumb.gif) .
в) Пусть событие С состоит в том, что все выбранные изделия бракованные. Количество возможных способов взять 3 изделия из 25-ти равно
.
в) Пусть событие С состоит в том, что все выбранные изделия бракованные. Количество возможных способов взять 3 изделия из 25-ти равно 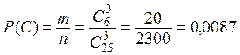 .
Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
.
Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
