-
Главная
-
Полезные советы
-
Напряжения и деформации при кручении круглого вала.
Напряжения и деформации при кручении круглого вала.
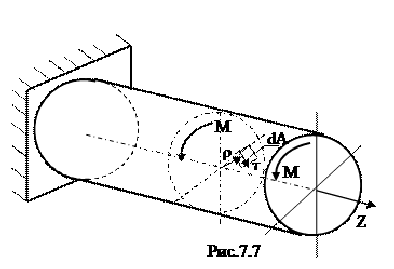
Рассмотрим брус круглого сечения, нагруженный парами сил в плоскости торцевого сечения (рис.7.7). В поперечных сечениях этого бруса возникает постоянный крутящий момент
М
кр =М или М
кр =
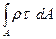
. (7.5).
Это уравнение позволит определить касательные напряжения, если известен их закон распределения по площади сечения. На основании результатов
экспериментов механизм деформирования бруса с круглым сечением основывается на следующих допущениях:
1) поперечные сечения бруса плоские и нормальные к оси до деформации остаются плоскими и нормальными после деформации, т.е. при кручении круглых валов справедлива гипотеза плоских сечений;
2) расстояния между любыми двумя сечениями в процессе деформации кручения не изменяется (ε
z = 0);
На основании этих допущений σ
х =σ
у =σ
z=τ
ху =0, поэтому в поперечных сечениях будут действовать только касательные напряжения τ
zx и τ
zу,следовательно, при кручении брус испытывает деформацию чистого сдвига.
Двумя поперечными сечениями выделим из вала элемент длиной dz , а из него затем выделим элементарное кольцо с радиусами ρ и ρ + dρ (рис. 7.8). Будем считать левое торцевое сечение неподвижным, тогда правое торцевое сечение кольца повернется под действием крутящего момента относительно левого на угол dφ. Образующая цилиндра АВ при этом повернётся на угол γ и займет положение
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0024_thumb.gif)
. С одной стороны дуга
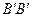 /
/ =ρdφ, с другой - В
/ В
/ = γdz, следовательно,
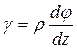
. (7.6)
Угол γ – это угол сдвига цилиндрической поверхности, а величина
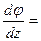
Θ называется относительным углом закручивания (аналогично
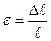
).
![clip_image001[4] clip_image001[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0014_thumb.gif)
По закону Гука для сдвига τ=Gγ, тогда
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0026_thumb.gif)
, откуда следует
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0044_thumb.gif)
(7.7)
Подставляя (7.7) в уравнение (7.5), получим
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0064_thumb.gif)
Так как
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0084_thumb.gif)
, то
![clip_image010[4] clip_image010[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0104_thumb.gif)
Учитывая, что
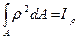
получим
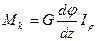
,
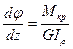
(а),
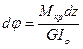
.
Из последнего выражения следует формула угла закручивания
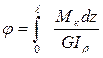
(7.8)
Если крутящий момент М
к и жесткость вала GІ
ρ по его длине не изменяются, то
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0028_thumb.gif)
![clip_image001[4] clip_image001[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0014_thumb.png)
Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала
![clip_image002[12] clip_image002[12]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image00212_thumb.gif)
![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0046_thumb.gif)
=
![clip_image006[6] clip_image006[6]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0066_thumb.gif)
(7.10)
Согласно этой формуле касательные напряжения в поперечном сечении вала распределяются вдоль радиуса по линейному закону, достигая наибольшей величины в точке наиболее удаленной от оси бруса (рис.7.9).
Согласно (7.10):
![clip_image002[16] clip_image002[16]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image00216_thumb.gif)
или
![clip_image004[10] clip_image004[10]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image00410_thumb.gif)
.
Введя обозначение
![clip_image006[10] clip_image006[10]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image00610_thumb.gif)
(момент сопротивления сечения при кручении), получим
![clip_image008[6] clip_image008[6]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0086_thumb.gif)
.
Для круглого сечения
![clip_image010[6] clip_image010[6]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0106_thumb.gif)
Материал вала возле оси недогружен, поэтому применяют пустотелые валы. При равных площадях поперечных сечений и одинаковом крутящем моменте в пустотелом вале напряжения будут меньше, а при равных напряжениях в пустотелом вале крутящий момент будет больше.
Для такого вала
![clip_image012[4] clip_image012[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0124_thumb.gif)
, где D- наружный диаметр, d – внутренний диаметр вала,
![clip_image014[4] clip_image014[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0144_thumb.gif)
,
![clip_image016[4] clip_image016[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0164_thumb.gif)
.
Если испытываете трудности в написании
курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
 Мкр =М или Мкр =
Мкр =М или Мкр =![clip_image001[4] clip_image001[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0014_thumb.gif) По закону Гука для сдвига τ=Gγ, тогда
По закону Гука для сдвига τ=Gγ, тогда 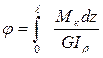 (7.8)
Если крутящий момент Мк и жесткость вала GІρ по его длине не изменяются, то
(7.8)
Если крутящий момент Мк и жесткость вала GІρ по его длине не изменяются, то ![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0028_thumb.gif)
![clip_image001[4] clip_image001[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0014_thumb.png) Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала
Вернёмся к выражению (7.7). Используя уравнение (а), получим формулу касательных напряжений при кручении круглого вала ![clip_image004[10] clip_image004[10]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image00410_thumb.gif) .
Введя обозначение
.
Введя обозначение ![clip_image016[4] clip_image016[4]](https://moscow-stud.com/wp-content/uploads/4f7280a92c7e_A97C/clip_image0164_thumb.gif) .
Если испытываете трудности в написании курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
.
Если испытываете трудности в написании курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
