-
Главная
-
Полезные советы
-
Нелинейная регрессия и корреляция
Нелинейная регрессия и корреляция
Различают 2 класса нелинейных регрессий:
1. Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам
– полиномы различных степеней –
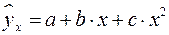
,
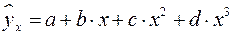
;
– равносторонняя гипербола –
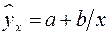
;
– полулогарифмическая функция –
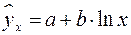
.
2. Нелинейные по оцениваемым параметрам
– степенная –
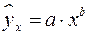
;
– показательная –
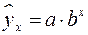
;
– экспоненциальная –
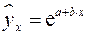
.
Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов.
Регрессии, нелинейные по оцениваемым параметрам, делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).
К внутренне линейным моделям относятся, например, степенная функция –
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0024_thumb.gif)
, показательная –
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0044_thumb.gif)
, экспоненциальная –
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0064_thumb.gif)
, логистическая –
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0084_thumb.gif)
, обратная –
![clip_image010[4] clip_image010[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0104_thumb.gif)
.
К внутренне нелинейным моделям можно, например, отнести следующие модели:
![clip_image012[4] clip_image012[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0124_thumb.gif)
,
![clip_image014[4] clip_image014[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0144_thumb.gif)
.
Среди нелинейных моделей наиболее часто используется степенная функция
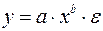
, которая приводится к линейному виду логарифмированием:
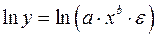
;
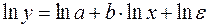
;
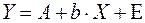
,
где
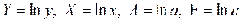
.
Широкое использование степенной функции связано с тем, что параметр
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0026_thumb.gif)
в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид:
![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0046_thumb.gif)
. (1.19)
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора
![clip_image006[6] clip_image006[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0066_thumb.gif)
, то обычно рассчитывается средний коэффициент эластичности:
![clip_image008[6] clip_image008[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0086_thumb.gif)
. (1.20)
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.5
Вид функции, ![clip_image002[14] clip_image002[14]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00214_thumb.gif) |
Первая производная, ![clip_image004[14] clip_image004[14]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00414_thumb.gif) |
Средний коэффициент эластичности, ![clip_image006[14] clip_image006[14]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00614_thumb.gif) |
| 1 |
2 |
3 |
![clip_image008[14] clip_image008[14]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00814_thumb.gif) |
![clip_image010[18] clip_image010[18]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01018_thumb.gif) |
![clip_image012[12] clip_image012[12]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01212_thumb.gif) |
![clip_image014[12] clip_image014[12]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01412_thumb.gif) |
![clip_image016[10] clip_image016[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01610_thumb.gif) |
![clip_image018[10] clip_image018[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01810_thumb.gif) |
![clip_image020[10] clip_image020[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image02010_thumb.gif) |
![clip_image022[10] clip_image022[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image02210_thumb.gif) |
![clip_image024[10] clip_image024[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image02410_thumb.gif) |
![clip_image026[6] clip_image026[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0266_thumb.gif) |
![clip_image028[6] clip_image028[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0286_thumb.gif) |
![clip_image010[19] clip_image010[19]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01019_thumb.gif) |
![clip_image030[6] clip_image030[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0306_thumb.gif) |
![clip_image032[6] clip_image032[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0326_thumb.gif) |
![clip_image034[6] clip_image034[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0346_thumb.gif) |
![clip_image036[6] clip_image036[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0366_thumb.gif) |
![clip_image038[6] clip_image038[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0386_thumb.gif) |
![clip_image040[6] clip_image040[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0406_thumb.gif) |
![clip_image042[6] clip_image042[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0426_thumb.gif) |
![clip_image044[6] clip_image044[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0446_thumb.gif) |
![clip_image046[6] clip_image046[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0466_thumb.gif) |
![clip_image048[6] clip_image048[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0486_thumb.gif) |
![clip_image050[6] clip_image050[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0506_thumb.gif) |
![clip_image052[6] clip_image052[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0526_thumb.gif) |
Расчет коэффициента эластичности не имеет смысла, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.
Уравнение нелинейной регрессии дополняется показателем тесноты связи - это индекс корреляции:
![clip_image002[16] clip_image002[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00216_thumb.gif)
, (1.21)
где
![clip_image004[16] clip_image004[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00416_thumb.gif)
– общая дисперсия результативного признака
![clip_image006[16] clip_image006[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00616_thumb.gif)
,
![clip_image008[16] clip_image008[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00816_thumb.gif)
– остаточная дисперсия.
Величина данного показателя находится в пределах:
![clip_image010[22] clip_image010[22]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01022_thumb.gif)
. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака
![clip_image006[17] clip_image006[17]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00617_thumb.gif)
, объясняемую регрессией, в общей дисперсии результативного признака:
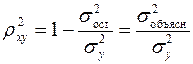
, (1.22)
т.е. имеет тот же смысл, что и в линейной регрессии;
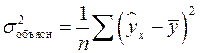
.
Индекс детерминации
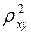
можно сравнивать с коэффициентом детерминации
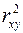
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина
![clip_image019[1] clip_image019[1]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0191_thumb.gif)
меньше
![clip_image017[1] clip_image017[1]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0171_thumb.gif)
. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
Индекс детерминации используется для проверки существенности в целом уравнения регрессии по F-критерию Фишера:
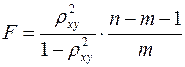
,
где
![clip_image017[2] clip_image017[2]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0172_thumb.gif)
– индекс детерминации,
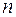
– число наблюдений,
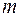
– число параметров при переменной
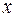
. Фактическое значение F-критерия (1.23) сравнивается с табличным при уровне значимости
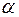
и числе степеней свободы
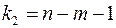
(для остаточной суммы квадратов) и
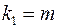
(для факторной суммы квадратов).
О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая вычисляется по той же формуле как и в линейном случае.
Если испытываете трудности в написании
курсовой работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0084_thumb.gif) , обратная –
, обратная – ![clip_image010[4] clip_image010[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0104_thumb.gif) .
К внутренне нелинейным моделям можно, например, отнести следующие модели:
.
К внутренне нелинейным моделям можно, например, отнести следующие модели: ![clip_image014[4] clip_image014[4]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0144_thumb.gif) .
Среди нелинейных моделей наиболее часто используется степенная функция
.
Среди нелинейных моделей наиболее часто используется степенная функция ![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0046_thumb.gif) . (1.19)
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора
. (1.19)
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора ![clip_image008[6] clip_image008[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0086_thumb.gif) . (1.20)
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.5
. (1.20)
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.5
![clip_image012[12] clip_image012[12]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01212_thumb.gif)
![clip_image018[10] clip_image018[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image01810_thumb.gif)
![clip_image020[10] clip_image020[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image02010_thumb.gif)
![clip_image024[10] clip_image024[10]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image02410_thumb.gif)
![clip_image040[6] clip_image040[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0406_thumb.gif)
![clip_image042[6] clip_image042[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0426_thumb.gif)
![clip_image044[6] clip_image044[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0446_thumb.gif)
![clip_image046[6] clip_image046[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0466_thumb.gif)
![clip_image048[6] clip_image048[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0486_thumb.gif)
![clip_image050[6] clip_image050[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0506_thumb.gif)
![clip_image052[6] clip_image052[6]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image0526_thumb.gif)
![clip_image002[16] clip_image002[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00216_thumb.gif) , (1.21)
где
, (1.21)
где ![clip_image004[16] clip_image004[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00416_thumb.gif) – общая дисперсия результативного признака
– общая дисперсия результативного признака ![clip_image008[16] clip_image008[16]](https://moscow-stud.com/wp-content/uploads/9f56b5243457_10131/clip_image00816_thumb.gif) – остаточная дисперсия.
Величина данного показателя находится в пределах:
– остаточная дисперсия.
Величина данного показателя находится в пределах: 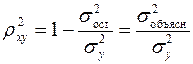 , (1.22)
т.е. имеет тот же смысл, что и в линейной регрессии;
, (1.22)
т.е. имеет тот же смысл, что и в линейной регрессии; 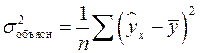 .
Индекс детерминации
.
Индекс детерминации 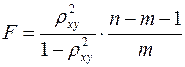 ,
где
,
где 