1. Главная
2. Полезные советы
3. Нелинейная регрессия и линеаризация

Нелинейная регрессия и линеаризация

Линеаризация уравнения регрессии путем замены переменных

Многие экономические явления описываются нелинейными уравнениями лучшим способом, чем линейные уравнения. И в этом случае мы не можем применить к ним обычный МНК, и используем стандартные подходы к оценке стат. надежности. В связи с этим встает задача по возможности привести нелинейное уравнение к линейному виду. 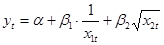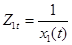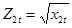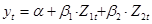В тех случаях, когда нелинейность касается факторных переменных, но не связана с нелинейностью коэффициентов уравнения регрессии, нелинейность обычно устраняется путем замены переменных: вводим новую переменную: и Следовательно , т. е. линейное уравнение. Во всех случаях, когда можно вычислить новую переменную с использованием информации об исходной переменной до определения параметров уравнения регрессии. Метод замены переменных решает поставленные задачи линеаризацией уравнения регрессии.

Линеаризация уравнения регрессии с использованием логарифмического преобразования (степенные и показательные функции)

В тех случаях, когда связь между факторами перем-ми и результ-им приз-ом имеет вид степенного уравнения (мультиколлинеарная функция) линеаризация производится путем логарифмирования исходного уравнения.

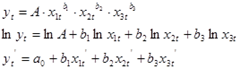
Представление случайного члена в преобразованных нелинейных уравнениях регрессии

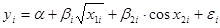
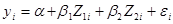
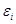
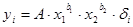
(1) (2) Если в (1) удовлетворяет четырем условиям случайности, т. е. мат. ожидание =0, независимо друг от друга, то случайная составляющая во (2) также будет удовлетворять этим условиям, и найденные из (2) с помощью МНК оценки параметров будут несмещенными, состоятельными и эффективными оценками. Если будем иметь уравнение вида: (3) , то случайная составляющая должна входить как сомножитель. (4) Если испытываете трудности в написании контрольной работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.