1. Главная
2. Полезные советы
3. Нормальное напряжение при чистом изгибе.

Нормальное напряжение при чистом изгибе.

Изгиб изучается в главных центральных осях, поэтому оси Х и У – главные центральные. Чтобы согласовать знак нормальных напряжений со знаком изгибающего момента ось У направлена вниз. Запишем уравнения равновесия левой части рассматриваемой балки. ΣΧ=0 (6.1), ΣУ=0 (6.2), ΣZ==N =0 (6.3), ΣM_х==М (6.4), M_у==0 (6.5), ΣM_z= 0 (6.6). Уравнения (6.1), (6.2), (6.6) выполняются тождественно. Оставшиеся уравнения (6.3), (6.4), (6.5) имеют бесчисленное множество решений, т.к. они могут удовлетворятся при различных законах распределения нормальных напряжений по сечению. Таким образом, определение этих напряжений является статически неопределимой задачей. Для её решения рассмотрим закономерно деформаций при изгибе на примере бруса с прямоугольным сечением, которые при чистом изгибе легко обнаружить экспериментальным путём. Поперечные сечения плоские и перпендикулярные к оси до деформации, остаются плоскими и перпендикулярными к оси балки после деформации. Часть волокон растягивается, часть сжимается. Между ними имеются волокна, которые не изменяют своей длины, они образуют нейтральный слой (рис.6.17). Линия пересечения нейтрального слоя с поперечным сечением называется нейтральной линией. Рассмотрим элемент балки длиной dz. (рис. 6.18). Примем условно левый его торец за неподвижный, тогда правый повернётся относительно его на угол dΘ. Так как нейтральный слой своей длины не меняет, то CD=C₁D₁ = ρdΘ. Деформация произвольного отрезка АВ=dz, взятого на расстоянии y от нейтрального слоя, найдется из выражения: ε_АВ=, т.е. ε. Здесь -расстояние нейтрального слоя от центральной оси х. По закону Гука для одноосного растяжения (6.7). Это выражение представляет уравнение совместности деформаций, полученное на основе гипотезы плоских сечений и линейного напряженного состояния в поперечном сечении балки. Теперь уравнения равновесия (6.3), (6.4), (6.5) с учетом формулы (6.7) будут иметь единственное решение. , ≠0, следовательно, . Каждый из последних двух интегралов должен равняться нулю. Первый интеграл представляет статический момент площади так как он равен нулю, то нейтральная линия совпадает с центральной осью Х, во втором интеграле А≠0,следовательно, , т.е., нейтральный слой проходит через ось бруса. В этом случае (6.8). = , Центробежный момент инерции равен нулю, поэтому оси Х,У являются главными центральными. Уравнение (6.4): так как , то (6.9), - кривизна изогнутой оси балки. - жёсткость при изгибе. Подставив значение кривизны (6.9) в уравнение (6.8), получим (6.10). Это формула для нормальных напряжений при чистом изгибе. Из неё следует, что по ширине сечения нормальные напряжения не меняются, а по высоте (вдоль оси У) они меняются по линейному закону (рис.6.19).   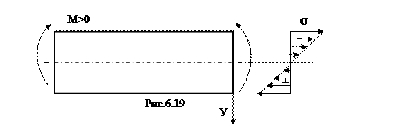Максимальные напряжения будут при у = у_max, т.е.,но - момент сопротивления изгибу, тогда . Эта формула позволяет записать условие прочности при изгибе по нормальным напряжениям при условии, что материал одинаково сопротивляется растяжению, сжатию: ≤ [σ]. (6.11) Из этого условия прочности может быть решен вопрос о размерах поперечного сечения балки≥ (6.12) и о её грузоподъёмности (6.13) Если испытываете трудности в написании курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.