-
Главная
-
Полезные советы
-
Определение опорных реакций. Решение задач.
Определение опорных реакций. Решение задач.
Балки предназначены для восприятия поперечных нагрузок. По способу приложения нагрузки делятся на сосредоточенные (действуют на точку) и распределенные (действуют на значительную площадь или длину).
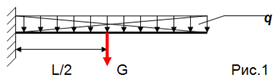 q
q - интенсивность нагрузки, кн/м
G =
q L – равнодействующая распределенной нагрузки
Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:
· Шарнирно-подвижная

Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.
· Шарнирно-неподвижная

Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими R
Aу и R
Aх вдоль осей координат.
· Жесткая заделка (защемление)

Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими R
Aу , R
Aх и моментом М
А. Для определения этих неизвестных удобно использовать систему уравнений.
∑ F
kx = 0
∑ F
kу = 0
∑ m
А(F
к)= 0
Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ m
В(F
к)= 0
Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G
= 0,4 кн приложена посередине балки.
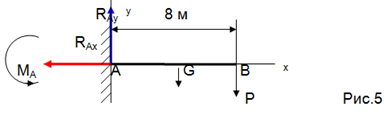
Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями . Выбираем координатные оси и составляем уравнения равновесия.
∑ F
kx = 0 R
Aх = 0
∑ F
kу = 0 R
Aу – G – P = 0
∑ m
А(F
к)= 0 - M
A + G L / 2 + P L = 0
Решая уравнения, получим R
Aу = G + P = 0,4 + 1 = 1,4 кн
M
A = G L / 2 + P L = 0,4
. 4 + 1
. 8 = 9,6 кн
. м
Проверяем полученные значения реакций:
∑ m
в(F
к)= 0 - M
A + R
AуL - G L / 2 = 0
- 9,6 + 1,4
. 8 – 0,4
. 4 = 0
- 11,2 + 11,2 = 0 реакции найдены верно.
Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.
∑ F
kх = 0
∑ m
А(F
к)= 0
∑ m
В(F
k)= 0
Для контроля правильности решения используется дополнительное уравнение ∑ F
kу = 0
Задача.
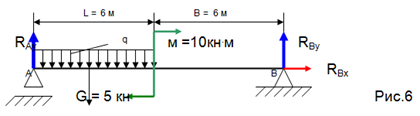
1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;
2) Заменяем распределенную нагрузку на равнодействующую G = q
. L;
3) Выбираем координатные оси;
4) Составляем уравнения равновесия.
∑ F
kx = 0 R
Вх = 0
∑ m
А(F
к)= 0 G
.L/2 + m - R
Ву (L + B)= 0
R
Ву = [G
.L/2 + m]/(L + B) = [5
. 6/2 + 10](6+6) = 2,08 кн
∑ m
В(F
k)= 0 R
Aу.(L + B) - Q
.(L/2 + B) + m = 0
R
Aу = [Q
.(L/2 + B) - m] / (L + B) =[5
.(6/2 + 6) - 10] / (6 + 6) = 2,92 кн
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
 q - интенсивность нагрузки, кн/м
G = q L – равнодействующая распределенной нагрузки
Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:
· Шарнирно-подвижная
q - интенсивность нагрузки, кн/м
G = q L – равнодействующая распределенной нагрузки
Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:
· Шарнирно-подвижная
 Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.
· Шарнирно-неподвижная
Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.
· Шарнирно-неподвижная
 Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими RAу и RAх вдоль осей координат.
· Жесткая заделка (защемление)
Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими RAу и RAх вдоль осей координат.
· Жесткая заделка (защемление)
 Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими RAу , RAх и моментом МА. Для определения этих неизвестных удобно использовать систему уравнений.
∑ Fkx = 0
∑ Fkу = 0
∑ mА(Fк)= 0
Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ mВ(Fк)= 0
Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G = 0,4 кн приложена посередине балки.
Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими RAу , RAх и моментом МА. Для определения этих неизвестных удобно использовать систему уравнений.
∑ Fkx = 0
∑ Fkу = 0
∑ mА(Fк)= 0
Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ mВ(Fк)= 0
Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G = 0,4 кн приложена посередине балки.
 Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями . Выбираем координатные оси и составляем уравнения равновесия.
∑ Fkx = 0 RAх = 0
∑ Fkу = 0 RAу – G – P = 0
∑ mА(Fк)= 0 - MA + G L / 2 + P L = 0
Решая уравнения, получим RAу = G + P = 0,4 + 1 = 1,4 кн
MA = G L / 2 + P L = 0,4 . 4 + 1. 8 = 9,6 кн . м
Проверяем полученные значения реакций:
∑ mв(Fк)= 0 - MA + RAуL - G L / 2 = 0
- 9,6 + 1,4. 8 – 0,4. 4 = 0
- 11,2 + 11,2 = 0 реакции найдены верно.
Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.
∑ Fkх = 0
∑ mА(Fк)= 0
∑ mВ(Fk)= 0
Для контроля правильности решения используется дополнительное уравнение ∑ Fkу = 0
Задача.
Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями . Выбираем координатные оси и составляем уравнения равновесия.
∑ Fkx = 0 RAх = 0
∑ Fkу = 0 RAу – G – P = 0
∑ mА(Fк)= 0 - MA + G L / 2 + P L = 0
Решая уравнения, получим RAу = G + P = 0,4 + 1 = 1,4 кн
MA = G L / 2 + P L = 0,4 . 4 + 1. 8 = 9,6 кн . м
Проверяем полученные значения реакций:
∑ mв(Fк)= 0 - MA + RAуL - G L / 2 = 0
- 9,6 + 1,4. 8 – 0,4. 4 = 0
- 11,2 + 11,2 = 0 реакции найдены верно.
Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.
∑ Fkх = 0
∑ mА(Fк)= 0
∑ mВ(Fk)= 0
Для контроля правильности решения используется дополнительное уравнение ∑ Fkу = 0
Задача.
 1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;
2) Заменяем распределенную нагрузку на равнодействующую G = q . L;
3) Выбираем координатные оси;
4) Составляем уравнения равновесия.
∑ Fkx = 0 RВх = 0
∑ mА(Fк)= 0 G .L/2 + m - RВу (L + B)= 0
RВу = [G .L/2 + m]/(L + B) = [5. 6/2 + 10](6+6) = 2,08 кн
∑ mВ(Fk)= 0 RAу.(L + B) - Q .(L/2 + B) + m = 0
RAу = [Q .(L/2 + B) - m] / (L + B) =[5 .(6/2 + 6) - 10] / (6 + 6) = 2,92 кн
Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;
2) Заменяем распределенную нагрузку на равнодействующую G = q . L;
3) Выбираем координатные оси;
4) Составляем уравнения равновесия.
∑ Fkx = 0 RВх = 0
∑ mА(Fк)= 0 G .L/2 + m - RВу (L + B)= 0
RВу = [G .L/2 + m]/(L + B) = [5. 6/2 + 10](6+6) = 2,08 кн
∑ mВ(Fk)= 0 RAу.(L + B) - Q .(L/2 + B) + m = 0
RAу = [Q .(L/2 + B) - m] / (L + B) =[5 .(6/2 + 6) - 10] / (6 + 6) = 2,92 кн
Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
