-
Главная
-
Полезные советы
-
Определите общую дисперсию заработной платы рабочих цеха; оцените однородность совокупности рабочих цеха по уровню месячной заработной платы.
Определите общую дисперсию заработной платы рабочих цеха; оцените однородность совокупности рабочих цеха по уровню месячной заработной платы.
По каждой из трех основных рабочих профессий цеха (
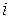
-порядковый номер профессии: 1-токари; 2-фрезеровщики; 3-слесари) имеются соответствующие данные о числе рабочих профессии (
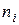
чел.), о средней заработной плате (
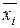
, руб.), а также о внутригрупповой дисперсии заработной платы (
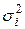
. руб
2). Статистические данные за месяц приведены в таблице.
Требуется:
1) определить общую дисперсию заработной платы рабочих цеха;
2) оценить однородность совокупности рабочих цеха по уровню месячной заработной платы;
3) определить, на сколько процентов дисперсия в размере заработной платы обусловлена различиями в профессии рабочих и влиянием других причин.
![clip_image002[1] clip_image002[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0021_thumb.gif) |
![clip_image004[1] clip_image004[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0041_thumb.gif) |
![clip_image006[1] clip_image006[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0061_thumb.gif) |
![clip_image008[1] clip_image008[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0081_thumb.gif) |
| 1 |
52 |
2650 |
2400 |
| 2 |
26 |
2780 |
3100 |
| 3 |
42 |
2420 |
730 |
Предварительные сведения.
Для характеристики величины вариации (колеблемости) признака статистической совокупности используются абсолютные и относительные показатели. В качестве абсолютных показателей чаще всего рассматривают дисперсию
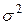
и среднеквадратическое отклонение
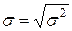
(СКО)
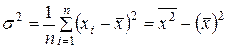
,
где
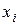
- наблюдённые значения признака (варианты),
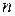
– общее число вариант (объем выборки). Суммирование в этой формуле производится по всем вариантам;
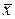
– среднее значение признака,
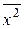
– среднее значение квадрата признака
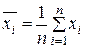
,
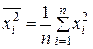
.
Изучая только общую дисперсию интересующего исследователя признака, нельзя оценить влияние отдельных факторов, как качественных, так и количественных, на величину признака. Это можно сделать при помощи метода группировки, когда варианты
![clip_image019[1] clip_image019[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0191_thumb.gif)
подразделяются на непересекающиеся группы по признаку-фактору. При этом, кроме общей средней
![clip_image023[1] clip_image023[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0231_thumb.gif)
по всей выборке, рассматриваются средние по отдельным группам
![clip_image006[2] clip_image006[2]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0062_thumb.gif)
и следующие показатели дисперсии:
1. общая дисперсия
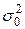
2. межгрупповая дисперсия
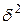
,
3. внутригрупповые дисперсии
![clip_image008[2] clip_image008[2]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0082_thumb.gif)
,
4. средняя внутригрупповая дисперсия
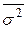
.
Кратко охарактеризуем эти дисперсии.
1. Общая дисперсия
![clip_image032[1] clip_image032[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0321_thumb.gif)
учитывает влияние всех факторов, от которых зависит величина изучаемого признака
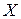
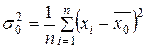
,
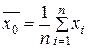
,
где
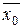
- общая средняя по всей выборке.
2. Межгрупповая дисперсия
![clip_image034[1] clip_image034[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0341_thumb.gif)
(дисперсия групповых средних) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Эта дисперсия определяется по формуле:
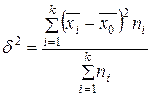
,
здесь
![clip_image006[3] clip_image006[3]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0063_thumb.gif)
– внутригрупповые средние,
![clip_image004[2] clip_image004[2]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0042_thumb.gif)
– число вариант в
![clip_image002[2] clip_image002[2]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0022_thumb.gif)
-ой группе;
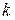
– число групп, суммирование производится по различным группам.
3. Внутригрупповая дисперсия
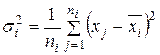
отражает рассеяние значений
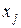
признака, относящихся к одному уровню группировочного фактора, поэтому она определяется не этим фактором, а другими причинами.
4. Средняя внутригрупповая дисперсия
![clip_image037[1] clip_image037[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0371_thumb.gif)
, так же как и
![clip_image008[3] clip_image008[3]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0083_thumb.gif)
, характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия, положенного в основу группировки. Эта дисперсия определяется по формуле
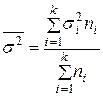
.
Можно доказать, что имеет место правило сложения дисперсий
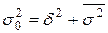
.
Отношение
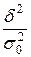
показывает, какую долю общей дисперсии составляет дисперсия, возникающая под влиянием группировочного фактора, т.е. позволяет оценить влияние этого фактора на величину изучаемого признака
![clip_image039[1] clip_image039[1]](https://moscow-stud.com/wp-content/uploads/565a8630b14e_E36B/clip_image0391_thumb.gif)
.
При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в разных совокупностях используются относительные показатели вариации. Наиболее распространенным среди относительных показателей вариации является коэффициент вариации
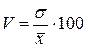
%.
Его применяют также и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Решение:
1. Найдем среднюю из внутригрупповых дисперсий
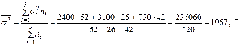
(руб
2)
Определим среднюю зарплату по цеху для основных рабочих профессий (общую среднюю)
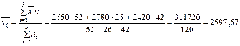
(руб.)
Находим межгрупповую дисперсию
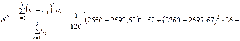
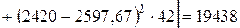
(руб
2).
Используя правило сложения дисперсий, найдем общую дисперсию заработной платы:
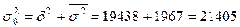
(руб
2).
2. Оценим однородность совокупности рабочих цеха по уровню месячной заработной платы с помощью коэффициента вариации
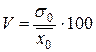
%
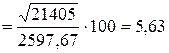
%.
Так как
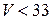
%, то совокупность считается однородной.
3. Общая дисперсия заработной платы рабочих цеха обусловлена различиями в профессии на
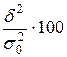
%
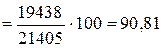
%.
Эта же дисперсия обусловлена влиянием других причин на
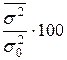
%
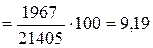
%.
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
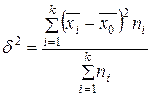 ,
здесь
,
здесь 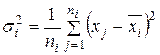 отражает рассеяние значений
отражает рассеяние значений 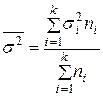 .
Можно доказать, что имеет место правило сложения дисперсий
.
Можно доказать, что имеет место правило сложения дисперсий
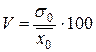 %
%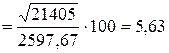 %.
Так как
%.
Так как 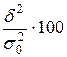 %
%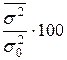 %
%