-
Главная
-
Полезные советы
-
Определите с помощью корреляционно-регрессионного анализа, есть ли связь между стажем работы и дневной выработки рабочего.
Определите с помощью корреляционно-регрессионного анализа, есть ли связь между стажем работы и дневной выработки рабочего.
Определите с помощью корреляционно-регрессионного анализа, есть ли связь между стажем работы и дневной выработки рабочего.
Таблица 18.1
| Номер рабочего |
Стаж работы, х |
Дневная выработка, у |
| 4-й |
1 |
4 |
| 6-й |
2 |
5 |
| 3-й |
3 |
6 |
| 1-й |
4 |
7 |
| 2-й |
5 |
7 |
| 7-й |
6 |
8 |
| 9-й |
7 |
8 |
| 10-й |
8 |
9 |
| 8-й |
9 |
10 |
| 5-й |
10 |
9 |
| итого |
Σх=55 |
Σу=73 |
Решение:
Произведем расчет в таблице
Таблица 18.2
| Номер рабочего |
Стаж работы, х |
Дневная выработка, у |
х2 |
у2 |
ху |
ŷ |
| исходные данные |
Расчетные данные |
| 4-й |
1 |
4 |
1 |
16 |
4 |
4,6 |
| 6-й |
2 |
5 |
4 |
25 |
10 |
5,2 |
| 3-й |
3 |
6 |
9 |
36 |
18 |
5,8 |
| 1-й |
4 |
7 |
16 |
49 |
28 |
6,4 |
| 2-й |
5 |
7 |
25 |
49 |
35 |
7,0 |
| 7-й |
6 |
8 |
36 |
64 |
48 |
7,0 |
| 9-й |
7 |
8 |
49 |
64 |
56 |
8,2 |
| 10-й |
8 |
9 |
64 |
81 |
72 |
8,8 |
| 8-й |
9 |
10 |
81 |
100 |
90 |
9,4 |
| 5-й |
10 |
9 |
100 |
81 |
90 |
10,0 |
| итого |
Σх=55 |
Σу=73 |
Σх2=385 |
Σу2=565 |
Σху=451 |
73 |
Для уточнения формы связи между рассматриваемыми признаками используем графический метод. Нанесем на график точки, соответствующие значениям х, у, получим корреляционное поле, а соединив их отрезками, — ломаную регрессии (рис. 18.1).
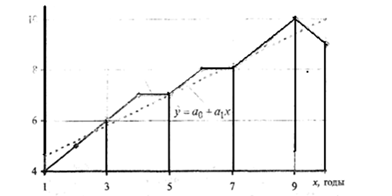
Рис.18.1. Зависимость выработки одного рабочего у от стажа работы х (по данным таблицы 18.1).
Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 18.1), которая может быть выражена простым линейным уравнением регрессии:
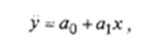
где х – стаж работы рабочих, годы; ŷ – теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии; а
1 – коэффициент регрессии, а
0- свободный член уравнения – параметры уравнения регрессии.
Пользуясь расчетными значениями (см. табл. 18.2), исчислим параметры для данного уравнения регрессии:
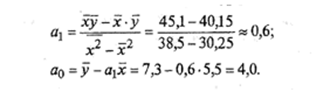
Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного уравнения регрессии:
ŷ =4+0,6х
Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значенияŷ
, найденные по данному уравнению, приведены в табл. 18.2. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм Σу=Σ ŷ (при этом возможно некоторое расхождение вследствие округления расчетов)
Рассмотрим вспомогательную таблицу (табл.18.3).
Таблица 18.3
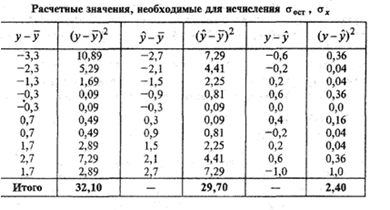
Средние квадратические отклонения (см. табл.16.2)
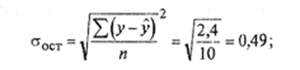
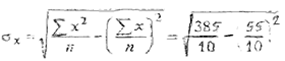
σ
х= 2,87
Расчетные значения t-критерия Стьюдента:
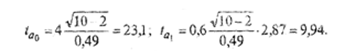
По таблице распределений Стьюдента для υ=8 находим критическое значение t-критерия Стьюдента (t
табл.=3,307 при α=0,05).
Поскольку расчетное значение больше табличного (t
расч. > t
табл.), оба параметра а
0 и а
1 признаются значимыми (отклоняется гипотеза о том, что каждый из этих параметров в действительности равен 0, и лишь в силу случайных обстоятельств оказался равным проверяемой величине).
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
 Рис.18.1. Зависимость выработки одного рабочего у от стажа работы х (по данным таблицы 18.1).
Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 18.1), которая может быть выражена простым линейным уравнением регрессии:
Рис.18.1. Зависимость выработки одного рабочего у от стажа работы х (по данным таблицы 18.1).
Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 18.1), которая может быть выражена простым линейным уравнением регрессии:
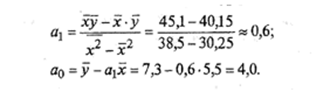 Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного уравнения регрессии:
ŷ =4+0,6х
Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значенияŷ, найденные по данному уравнению, приведены в табл. 18.2. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм Σу=Σ ŷ (при этом возможно некоторое расхождение вследствие округления расчетов)
Рассмотрим вспомогательную таблицу (табл.18.3).
Таблица 18.3
Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного уравнения регрессии:
ŷ =4+0,6х
Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значенияŷ, найденные по данному уравнению, приведены в табл. 18.2. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм Σу=Σ ŷ (при этом возможно некоторое расхождение вследствие округления расчетов)
Рассмотрим вспомогательную таблицу (табл.18.3).
Таблица 18.3
 Средние квадратические отклонения (см. табл.16.2)
Средние квадратические отклонения (см. табл.16.2)
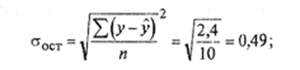
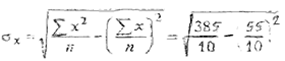 σх= 2,87
Расчетные значения t-критерия Стьюдента:
σх= 2,87
Расчетные значения t-критерия Стьюдента:
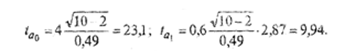 По таблице распределений Стьюдента для υ=8 находим критическое значение t-критерия Стьюдента (tтабл.=3,307 при α=0,05).
Поскольку расчетное значение больше табличного (tрасч. > tтабл.), оба параметра а0 и а1 признаются значимыми (отклоняется гипотеза о том, что каждый из этих параметров в действительности равен 0, и лишь в силу случайных обстоятельств оказался равным проверяемой величине).
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.
Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
По таблице распределений Стьюдента для υ=8 находим критическое значение t-критерия Стьюдента (tтабл.=3,307 при α=0,05).
Поскольку расчетное значение больше табличного (tрасч. > tтабл.), оба параметра а0 и а1 признаются значимыми (отклоняется гипотеза о том, что каждый из этих параметров в действительности равен 0, и лишь в силу случайных обстоятельств оказался равным проверяемой величине).
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.
Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
