-
Главная
-
Полезные советы
-
Определите: Среднюю стоимость основных фондов на 1 предприятие, Среднее квадратическое отклонение. Долю предприятий со стоимостью основных фондов более 50 млн. руб.
Определите: Среднюю стоимость основных фондов на 1 предприятие, Среднее квадратическое отклонение. Долю предприятий со стоимостью основных фондов более 50 млн. руб.
Для оценки стоимости основных фондов региона произведен 5% механический отбор, в результате чего установлено:
| Группы предприятий по стоимости основных фондов,млн. руб. |
До 10 |
10-20 |
20-30 |
30-40 |
40-50 |
50и более |
итого |
| Число предприятий |
131 |
227 |
294 |
146 |
128 |
74 |
1000 |
По включенным в выборку предприятиям определите:
· Среднюю стоимость основных фондов на 1 предприятие
· Среднее квадратическое отклонение.
· Долю предприятий со стоимостью основных фондов более 50 млн. руб.
· С вероятностью 0,954 пределы, в которых можно ожидать среднюю стоимость основных фондов на 1 предприятие.
· С вероятность 0,997 долю предприятий, со стоимостью основных фондов выше 50 млн. руб.
Решение.
Закроем открытые интервалы (1-ый и 6-ой), считая, что шаг интервала постоянный и равен 10.
Определим числовые характеристики выборки:
Таблица 3.1
| интервал |
xi |
ni |
wi |
xiwi |
xi –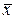 |
(xi –![clip_image002[1] clip_image002[1]](https://moscow-stud.com/wp-content/uploads/1.50_D5C8/clip_image0021_thumb.gif) )2 )2 |
wi (xi –![clip_image002[2] clip_image002[2]](https://moscow-stud.com/wp-content/uploads/1.50_D5C8/clip_image0022_thumb.gif) )2 )2 |
| 0-10 |
5 |
131 |
0,131 |
0,655 |
-20,215 |
408,646 |
53,533 |
| 10-20 |
10 |
227 |
0,227 |
2,27 |
-15,215 |
231,496 |
52,550 |
| 20-30 |
25 |
294 |
0,294 |
7,35 |
-0,215 |
0,046 |
0,014 |
| 30-40 |
35 |
146 |
0,146 |
5,11 |
9,785 |
95,746 |
13,979 |
| 40-50 |
45 |
128 |
0,128 |
5,76 |
19,785 |
391,446 |
50,105 |
| 50-60 |
55 |
74 |
0,074 |
4,07 |
29,785 |
887,146 |
65,649 |
| сумма |
- |
1000 |
1,000 |
25,215 |
- |
- |
235,829 |
xi– середина интервала,
ni– частота,
Относительная частота:
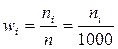
Выборочное среднее:
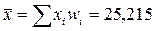
Выборочная дисперсия:
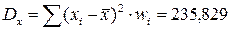
Выборочное среднее квадратическое отклонение:
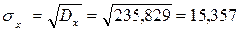
Теперь известно, что:
 σx
σx=15,357
σx2=235,829
n=1000 – объем выборки,
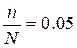
- т. к. выборка 5%,
N– объем генеральной совокупности.
Средняя ошибка механической выборки для среднего значения определяется по формуле ошибки случайной бесповторной выборки:
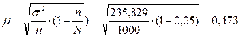
Предельная ошибка выборки для среднего значения:
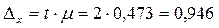
Где
t – кратность ошибки, зависит от доверительной вероятности.
p=0.954,
Ф(t)=p - функция Лапласа.
Определяем аргумент функции Лапласа по таблице приложения.
Ф(2)=0,954, следовательно
t=2.
Пределы, млн. руб.:
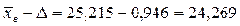
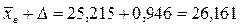
Средняя ошибка механической выборки для доли:
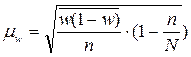 w
w=0.074 - доля предприятий со стоимостью основных фондов выше 50
млн. руб.
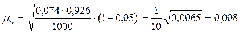
Предельная ошибка выборки для доли:
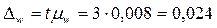 t
t– кратность ошибки, зависит от доверительной вероятности.
p=0.997,
Ф(t)=p - функция Лапласа.
Определяем аргумент функции Лапласа по таблице приложения.
Ф(3)=0,997, следовательно
t =3
Пределы для доли, доля 1:
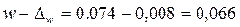
или 6,6%
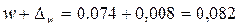
или 8,2%
Делаем вывод.
· Средняя стоимость основных фондов на одно предприятие в генеральной совокупности с вероятностью 0,954 находится в пределах: от 24,269 до 26,161 млн. руб.
· С вероятностью 0,997 в генеральной совокупности пределы для доли предприятий со стоимость основных фондов выше 50 млн. руб. составляют: от 6,6% до 8,2%.
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
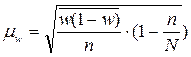 w=0.074 - доля предприятий со стоимостью основных фондов выше 50
млн. руб.
w=0.074 - доля предприятий со стоимостью основных фондов выше 50
млн. руб.
