-
Главная
-
Полезные советы
-
Перемещения при изгибе балки.
Перемещения при изгибе балки.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом перпендикулярными к изогнутой продольной оси (рис.6.23). Деформированная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям у(z) их центров тяжести сечений – прогибами балки. Прогибы у(z) и углы поворота сечений θ(z) связаны между собой. Из рис.6.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии, так как это углы с взаимно перпендикулярными сторонами. Согласно геометрическому смыслу первой производной у' =tgφ. Таким образом, tg θ = tgφ = у'.
В пределах упругих деформаций прогибы балок малы, а углы поворота не превышают 0,1 рад, поэтому можно принять θ= у'.
Форма упругой линии балки определяется выражения кривизны
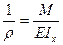
(α), полученной при выводе формулы нормальных напряжений.
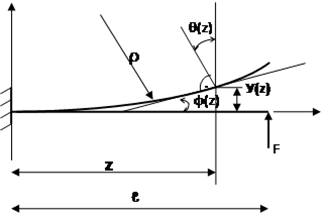
В тоже время кривизна плоской кривой равна
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/d014531198a9_CA57/clip_image0024_thumb.gif)
. (b)

Из равенства правых частей выражений (α) и (b) следует
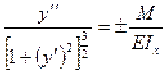
.
Полученное уравнение называется дифференциальным уравнением упругой линии балки. Как отмечалось выше, при малых деформациях (у')
2<<1, поэтому этой величиной можно пренебречь. В результате получим:
дифференциальное уравнение упругой линии балки
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/d014531198a9_CA57/clip_image0026_thumb.gif)
. (6.14)
Выбор знака в правой части этого уравнения определяется направлением оси У, так как от этого направления зависит знак второй производной
При ЕI
х=const, М=М( z)
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/d014531198a9_CA57/clip_image0044_thumb.gif)
=
![clip_image006[5] clip_image006[5]](https://moscow-stud.com/wp-content/uploads/d014531198a9_CA57/clip_image0065_thumb.gif)
,
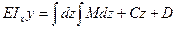
.
Постоянные интегрирования C и D определяются из граничных условий.
Если испытываете трудности в написании
курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
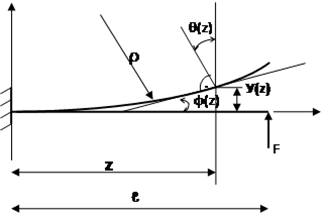
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/d014531198a9_CA57/clip_image0024_thumb.gif) . (b)
. (b) 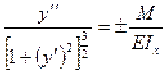 .
Полученное уравнение называется дифференциальным уравнением упругой линии балки. Как отмечалось выше, при малых деформациях (у')2<<1, поэтому этой величиной можно пренебречь. В результате получим:
дифференциальное уравнение упругой линии балки
.
Полученное уравнение называется дифференциальным уравнением упругой линии балки. Как отмечалось выше, при малых деформациях (у')2<<1, поэтому этой величиной можно пренебречь. В результате получим:
дифференциальное уравнение упругой линии балки ![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/d014531198a9_CA57/clip_image0026_thumb.gif) . (6.14)
Выбор знака в правой части этого уравнения определяется направлением оси У, так как от этого направления зависит знак второй производной
При ЕIх=const, М=М( z)
. (6.14)
Выбор знака в правой части этого уравнения определяется направлением оси У, так как от этого направления зависит знак второй производной
При ЕIх=const, М=М( z) 