-
Главная
-
Полезные советы
-
Построить гистограмму частот. Найти несмещенные оценки генеральной средней и генеральной дисперсии.
Построить гистограмму частот. Найти несмещенные оценки генеральной средней и генеральной дисперсии.
Дана таблица:

Задание:
1) построить гистограмму частот. Найти несмещенные оценки генеральной средней и генеральной дисперсии;
2) используя результаты пункта 1, обосновать гипотезу о нормальном распределении генеральной совокупности. Записать выражение соответствующего теоретического распределения;
3) вычислить для всех интервалов значений X соответствующие вероятности и теоретические частоты, используя критерий Пирсона (с уровнем значимости α = 0,1). Проверить обоснованную выше гипотезу;
4) в предположении, что выборка извлечена из нормально распределенной генеральной совокупности, найти доверительный интервал, заключающий генеральную среднюю признака с надежностью γ = 0,98.
Решение:
1) Объем выборки
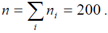
Величины всех интервалов одинаковы и равны h = 2 .
Для построения гистограммы частот составим таблицу.
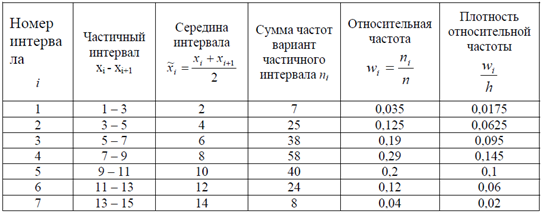
Гистограмма частот имеет следующий вид:
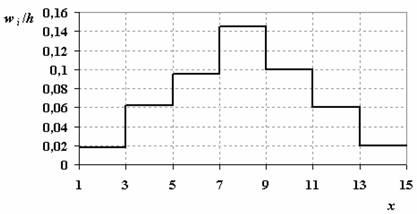
Несмещенные оценки генеральной средней B x и генеральной дисперсии s2 случайной величины Х найдем по формулам:
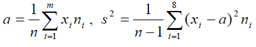
, где где xi – середина i-го интервала; m = 7.
Подставив данные из последней таблицы в расчетные формулы, получим:
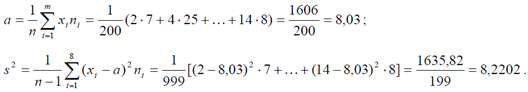
Определим также среднеее квадратическое отклонение s случайной величины Х по формуле:
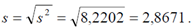
2) Рассмотрение полученной гистограммы частот позволяет предположить гипотезу о нормальном распределении генеральной совокупности. Выражение
плотности соответствующего теоретического распределения имеет вид
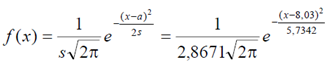
3) Проверить предложенную выше гипотезу о нормальности распределения, используя критерий Пирсона (с уровнем значимости α = 0,1).
Для расчета вероятностей pi попадания случайной величины X в интервалы
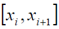
используем функцию Лапласа в соответствии со свойством
нормального распределения:
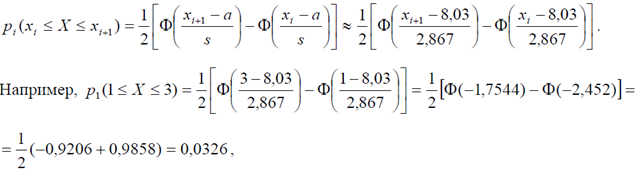
и, соответствующая первому интервалу теоретическая частота 200 0,0326 6,515 1 np = ⋅ = и т.д.
Для определения расчетной статистики
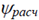
удобно составить таблицу:
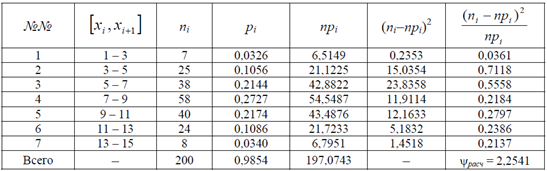
Итак, расчетное значение статистики
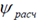
= 2,254. Поскольку число интервалов m = 7, а нормальный закон распределения определяется S = 2 параметрами,
то число степеней свободы k = m − S −1 = 7 − 2 −1 = 4 . Соответствующие верхнее и нижнее критические значения статистики определим из статистической
таблицы:
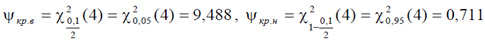
Т.к.
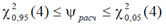
, гипотеза о выбранном теоретическом нормальном законе с параметрами a = 8,03 ; s = 2,867 согласуется с опытными данными.
4) Доверительный интервал для генеральной средней равен

Подставив исходные данные, получим:
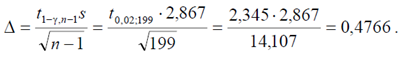
Отсюда доверительный интервал, заключающий генеральную среднюю признака с надежностью γ = 0,98, равен
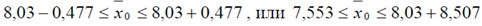
Если испытываете трудности в написании
контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
 Гистограмма частот имеет следующий вид:
Гистограмма частот имеет следующий вид:
 Несмещенные оценки генеральной средней B x и генеральной дисперсии s2 случайной величины Х найдем по формулам:
Несмещенные оценки генеральной средней B x и генеральной дисперсии s2 случайной величины Х найдем по формулам: 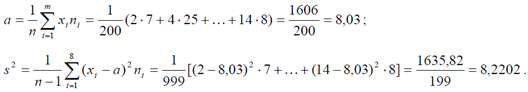 Определим также среднеее квадратическое отклонение s случайной величины Х по формуле:
Определим также среднеее квадратическое отклонение s случайной величины Х по формуле: 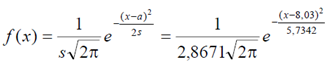 3) Проверить предложенную выше гипотезу о нормальности распределения, используя критерий Пирсона (с уровнем значимости α = 0,1).
Для расчета вероятностей pi попадания случайной величины X в интервалы
3) Проверить предложенную выше гипотезу о нормальности распределения, используя критерий Пирсона (с уровнем значимости α = 0,1).
Для расчета вероятностей pi попадания случайной величины X в интервалы 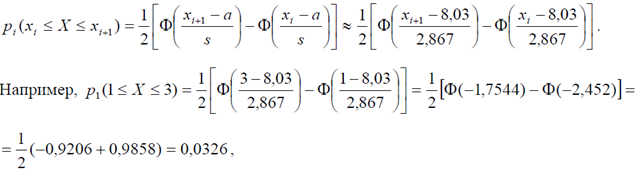 и, соответствующая первому интервалу теоретическая частота 200 0,0326 6,515 1 np = ⋅ = и т.д.
Для определения расчетной статистики
и, соответствующая первому интервалу теоретическая частота 200 0,0326 6,515 1 np = ⋅ = и т.д.
Для определения расчетной статистики  Итак, расчетное значение статистики
Итак, расчетное значение статистики  Подставив исходные данные, получим:
Подставив исходные данные, получим:
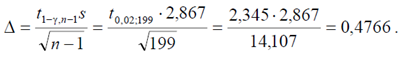 Отсюда доверительный интервал, заключающий генеральную среднюю признака с надежностью γ = 0,98, равен
Отсюда доверительный интервал, заключающий генеральную среднюю признака с надежностью γ = 0,98, равен
