-
Главная
-
Полезные советы
-
Произвольная пространственная система сил.
Произвольная пространственная система сил.
Система сил называется пространственной, если линии действия сил не лежат в одной плоскости. В этом случае систему также можно привести к центру, заменив ее одной силой, равной главному вектору, и парой с моментом, равным главному моменту относительно центра приведения, однако в общем случае сила не будет лежать в плоскости результирующей пары. Главный вектор системы сил найдется через его проекции на оси координат Х,У,Z.
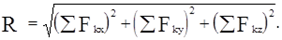
(1.11)
Модуль главного момента системы можно найти через моменты силы относительно осей координат:
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/a5e2051398f8_D189/clip_image0026_thumb.png)
(1.12)
Пространственная система сил будет эквивалентна нулю, то есть находиться в равновесии, если величины R и М
0, будут равны нулю. На этом основании следует шесть уравнений равновесия:
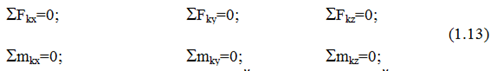
то есть для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси Х,У,Z и суммы моментов всех сил относительно этих осей были равны нулю.
Пример. Определить реакции шарниров и усилие в стержне, с помощью которых вагонная полка весом 200Н крепится к стене (рис.1.32).
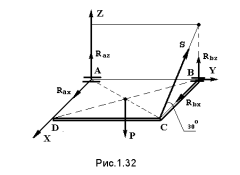
Решение.
Объект равновесия плита ABCD. Нагрузка на плиту - вес Р, приложен в центре плиты. Отбрасывая связи - шарниры А и В, прикладываем реакции, которые разлагаем на две составляющие -
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/a5e2051398f8_D189/clip_image0028_thumb.png)
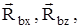
поскольку шарниры препятствуют перемещению плиты в плоскости XOZ. Реакция стержня S направлена вдоль стержня. На плиту действует пространственная система сил, для которой можно составить шесть уравнений равновесия. Выбираем оси координат и составляем уравнения.

Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
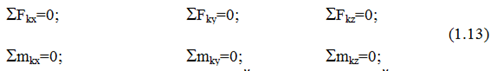 то есть для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси Х,У,Z и суммы моментов всех сил относительно этих осей были равны нулю.
Пример. Определить реакции шарниров и усилие в стержне, с помощью которых вагонная полка весом 200Н крепится к стене (рис.1.32).
то есть для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси Х,У,Z и суммы моментов всех сил относительно этих осей были равны нулю.
Пример. Определить реакции шарниров и усилие в стержне, с помощью которых вагонная полка весом 200Н крепится к стене (рис.1.32).
 Решение.
Объект равновесия плита ABCD. Нагрузка на плиту - вес Р, приложен в центре плиты. Отбрасывая связи - шарниры А и В, прикладываем реакции, которые разлагаем на две составляющие -
Решение.
Объект равновесия плита ABCD. Нагрузка на плиту - вес Р, приложен в центре плиты. Отбрасывая связи - шарниры А и В, прикладываем реакции, которые разлагаем на две составляющие -  Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
