-
Главная
-
Полезные советы
-
Расчёт на прочность при продольно-поперечном изгибе.
Расчёт на прочность при продольно-поперечном изгибе.
Условие прочности при поперечном изгибе
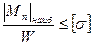
получено в предположении, что внутренние усилия
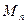
изменяются пропорционально изменению внешних сил. Как установлено ранее, при продольно-поперечном изгибе эта зависимость нелинейная.
Предполагая, что моменты пропорциональны прогибам, можно записать
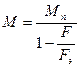 (8.10)
(8.10)
Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают пропорционально, тогда справедливы отношения
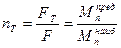 (8.11)
(8.11)
Здесь
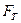
и
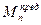
нагрузки, при которых в балке напряжения достигают предела текучести
(
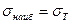
). Из (8.11) следует
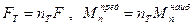
.
Наибольшие напряжения при поперечном изгибе с растяжением вычисляются по формуле
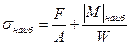
=
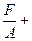
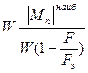
.
При достижении предельного состояния они будут равны
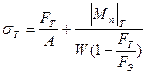
=
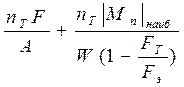
.
Разделив правую и левую часть этого уравнения на коэффициент запаса по текучести
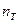
, получим
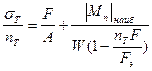
.
Так как
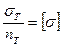
, то условие прочности при продольно-поперечном изгибе примет вид
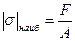
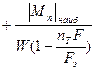
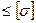
.
(8.12)
Нелинейность в этом выражении определяется коэффициентом
![clip_image028[1] clip_image028[1]](https://moscow-stud.com/wp-content/uploads/3a3ad67d24c0_8FC8/clip_image0281_thumb.gif)
. За счёт этой нелинейности левая часть условия прочности будет несколько меньше.
Если испытываете трудности в написании
курсовой работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
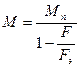 (8.10)
Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают пропорционально, тогда справедливы отношения
(8.10)
Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают пропорционально, тогда справедливы отношения
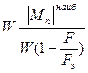 .
При достижении предельного состояния они будут равны
.
При достижении предельного состояния они будут равны 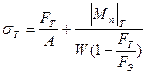 =
=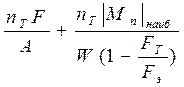 .
Разделив правую и левую часть этого уравнения на коэффициент запаса по текучести
.
Разделив правую и левую часть этого уравнения на коэффициент запаса по текучести 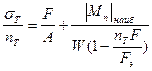 .
Так как
.
Так как