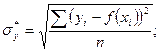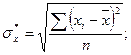-
Главная
-
Полезные советы
-
Проведите аппроксимацию пяти пар случайных чисел линейной зависимостью
Проведите аппроксимацию пяти пар случайных чисел линейной зависимостью
На основе имеющихся данных проведите аппроксимацию пяти пар случайных чисел линейной зависимостью.
Таблица 3.1
Решение:
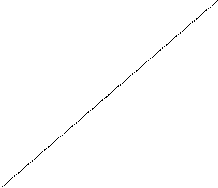
Экспериментальные точки, координаты которых представлены в таблице 3.1, представим в системе координат на рис.3.1.
 у
у





 9 •
9 •
 7 •
7 •
 4 •
4 •
 2 •
2 •
 1 •
1 •

1 2 3 4 5 х
Для проведения аппроксимации проведём предварительные вычисления.
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/9f94d073fd91_DAAB/clip_image0024_thumb.gif)
![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/9f94d073fd91_DAAB/clip_image0046_thumb.gif)
![clip_image006[3] clip_image006[3]](https://moscow-stud.com/wp-content/uploads/9f94d073fd91_DAAB/clip_image0063_thumb.gif)
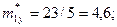
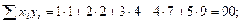
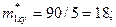
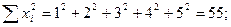
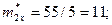
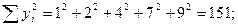
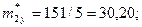
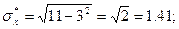
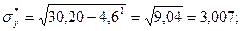
Вычислим коэффициент линейной корреляции.
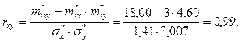
По статистическим таблицам найдём критическое значение критерия Стьюдента
tкрит=3,1814 при
n-2=5-2=3 степенях свободы и рекомендуемому уровню значимости α=0,05.
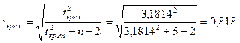
Ввиду того, что
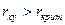
делаем заключение, что корреляционная связь между переменными
х и
у является существенной и она может быть линейной.
Вычислим коэффициенты линейной зависимости по формулам:
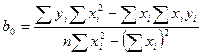
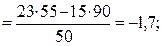
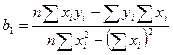
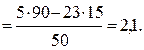
Таким образом, получили линейное уравнение регрессии:
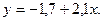
По уравнению регрессии по двум точкам построим функцию в системе координат на рис.3.1 и вычислим значения функции по экспериментальным значениям аргумента
х и разницу между экспериментальными и вычисленными значениями функции, которые представим в таблице 3.2.
Таблица 3.2
| хi |
yi |
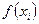 |
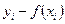 |
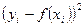 |
| 1 |
1 |
0,4 |
0,6 |
0,36 |
| 2 |
2 |
2.5 |
-0,5 |
0,25 |
| 3 |
4 |
4,6 |
-0,6 |
0,36 |
| 4 |
7 |
6,7 |
0,3 |
0,09 |
| 5 |
9 |
8,8 |
0,2 |
0,04 |
Вычислим стандартную ошибку и отношение стандартной ошибки к среднему значению:
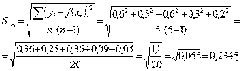
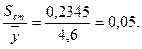
По отношению стандартной ошибки к среднему значению получен удовлетворительный результат, так как не превышено значение в 0.05.
Проведём оценку уровня значимости коэффициентов уравнения регрессии по критерию Стьюдента:
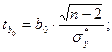
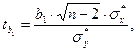
где
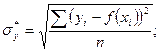
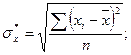
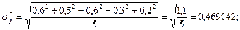
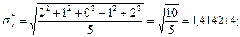
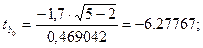
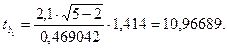
По статистической таблице находим критическое значение критерия Стьюдента
tкрит=3,183 для

3 степеней свободы и рекомендуемого уровня значимости
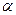
=0,05. Отметим, что по уровню значимости для коэффициентов
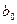
и
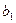
получен удовлетворительный результат, так как они по абсолютному значению превышают критическое значение.
Проведём оценку качества полученного уравнения регрессии по показателям, вычисляемым на основе дисперсионного анализа:
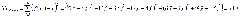
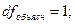
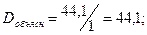
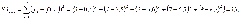
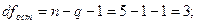
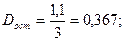
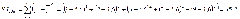
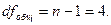
Проверка:
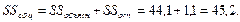
Результат проверки – положительный, что свидетельствует о корректности проведённых вычислений.
Вычислим критерий Фишера:
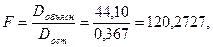
при двух степенях свободы:
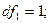
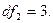
По статистическим таблицам находим критическое значение критерия
Фишера для рекомендуемого уровня значимости α=0.05
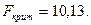
Так как вычисленное значение критерия Фишера превосходит критическое, то будем считать уровень значимости по критерию Фишера удовлетворительным.
Вычислим коэффициент множественной детерминации:
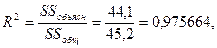
для двух степеней свободы
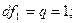
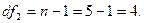
По статистической таблице для уровня значимости
0,05 находим критическое значение коэффициента множественной детерминации:
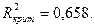
Так как вычисленное значение коэффициента множественной детерминации превышает критическое значение, то полученный результат по данному показателю будем считать удовлетворительным.
Таким образом, все полученные расчётные показатели по оценке качества уравнения регрессии являются удовлетворительными, поэтому будем считать результаты аппроксимации приемлемыми.
Если испытываете трудности в написании
курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
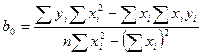
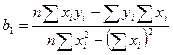
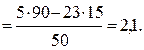 Таким образом, получили линейное уравнение регрессии:
Таким образом, получили линейное уравнение регрессии: 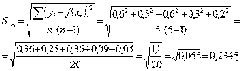
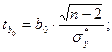
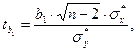 где
где