-
Главная
-
Полезные советы
-
Расчет конических зубчатых передач на контактную прочность
Расчет конических зубчатых передач на контактную прочность
Основными причинами выхода из строя конических колес являются усталостное выкрашивание материала с рабочих поверхностей зуба и поломка зубьев вследствие усталости.
Расчет производится так же как расчет цилиндрической косозубой передачи с эквивалентными зубчатыми колесами
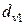
и
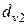
в среднем сечении зуба. Такой метод позволяет использовать ранее полученные зависимости.
В исходной формуле Герца заменим приведенный радиус кривизны
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0024_thumb.gif)
, найденный из рис. 20.
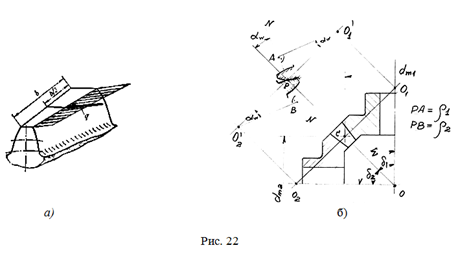
Здесь в сечении О
1О
2 в полюсе зацепления
Р отрезок АР соответствует радиусу кривизны шестерни
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0026_thumb.gif)
, а отрезок ВР – радиусу кривизны колеса
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0044_thumb.gif)
.
Рассматривая прямоугольные треугольники
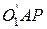
и
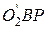
, оставляя только знак суммы (+), поскольку конические передачи бывают только с внешним зацеплением, получим:
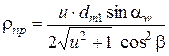
(4.9)
Далее полагаем, что для однопарного зацепления, как было показано ранее, известны нормальная нагрузка
qH и приведенный модуль упругости
Епр.
Из формулы для приведенного радиуса (4.9) следует, что его величина изменяется пропорционально среднему диаметру, а значит отношение q
H/r
пр постоянно и, следовательно, постоянно контактное напряжение в любом сечении. Поэтому за расчетное принимают среднее сечение зуба. В дополнение к этому, введем коэффициент прочности конических передач
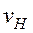
, учитывающий конструкцию зубчатых конических колес.
Принимая во внимание эти особенности, после подстановок в формулу Герца, получим формулу для проверочного расчета на контактную прочность любых конических передач:
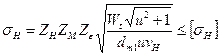
(4.10)
Здесь
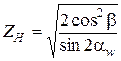
- коэффициент формы сопряженных поверхностей зубьев. Для
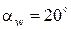
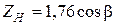
, где β - угол наклона зуба. Если колесо с круговой формой зуба, то обычно принимают
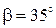
.
Для стальных колес
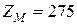
МПа
½.
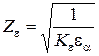
- коэффициент, учитывающий длину контактной линии зацепления конических колес. Обычно
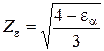
.
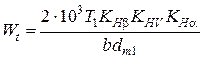
- удельная окружная сила.
Коэффициент
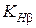
зависит от
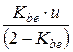
и определяется по графикам на рис.23 в зависимости от конструктивной схемы конической передачи, типа опор колес –
Iш (шариковые),
Iр (роликовые), а также твердости материала колес.
Здесь:
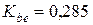
,
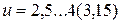
. Сплошные и штрихпунктирные линии относятся к коническим передачам с прямыми зубьями.
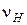
- коэффициент прочности конических передач. Определяется по таблице 13 в зависимости от вида конической передачи, твердости материала колес и передаточного числа:
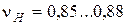
для прямозубых конических колес;
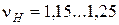
для конических колес с круговыми зубьями.
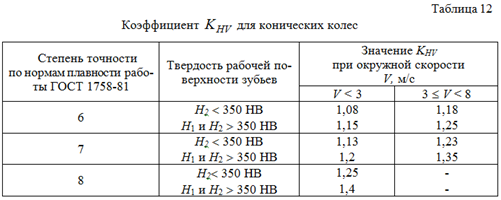
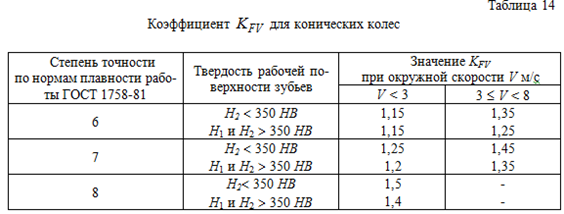
Коэффициент динамичности нагрузки -
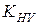
для конических колес находится по таблице 12. Он зависит от степени точности по нормам плавности работы передачи и окружной скорости колес.
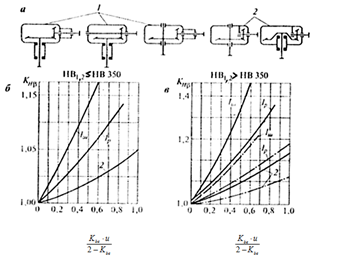
Рис. 23. Изменение коэффициентов
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0028_thumb.gif)
в зависимости от конструктивных соотношений в коническом зацеплении и твердости зубьев.
а) схемы передач; абсцисса на графиках
![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0046_thumb.gif)
;
б) для зубьев с твердостью ![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0064_thumb.gif)
;
в) для зубьев с твердостью ![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0084_thumb.gif)

Коэффициент неравномерности нагрузки зубьев
![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image00210_thumb.gif)
для колес с круговой формой зуба определяют по графику рис. 23 в зависимости от степени точности по
нормам плавности работы.
Для прямозубых конических передач
![clip_image004[8] clip_image004[8]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0048_thumb.gif)
,
![clip_image006[6] clip_image006[6]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0066_thumb.gif)
- диаметр в среднем сечении зуба шестерни.
Обозначив
![clip_image002[12] clip_image002[12]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image00212_thumb.gif)
и решая уравнение (15) относительно
![clip_image004[10] clip_image004[10]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image00410_thumb.gif)
, получим
для проектного расчета формулу расчета диаметра в среднем сечении конической шестерни, одного из главных геометрических параметров:
![clip_image006[8] clip_image006[8]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0068_thumb.gif)
, мм. (4.11)
Здесь
Кd - вспомогательный коэффициент. Для конических прямозубых передач
![clip_image008[6] clip_image008[6]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0086_thumb.gif)
(МПа)
1/3, и
Kd = 590…520 (МПа)
1/3 для передач с круговыми зубьями (
![clip_image010[6] clip_image010[6]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0106_thumb.gif)
); величина коэффициента относительной ширины зубчатого венца
![clip_image012[4] clip_image012[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0124_thumb.gif)
или
![clip_image014[4] clip_image014[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0144_thumb.gif)
, при условии пропорциональности ширины колес конусному расстоянию
![clip_image016[4] clip_image016[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0164_thumb.gif)
.
Если испытываете трудности в написании
курсовой работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0024_thumb.gif) , найденный из рис. 20.
, найденный из рис. 20.
 Здесь в сечении О1О2 в полюсе зацепления Р отрезок АР соответствует радиусу кривизны шестерни
Здесь в сечении О1О2 в полюсе зацепления Р отрезок АР соответствует радиусу кривизны шестерни 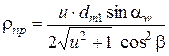 (4.9)
Далее полагаем, что для однопарного зацепления, как было показано ранее, известны нормальная нагрузка qH и приведенный модуль упругости Епр.
Из формулы для приведенного радиуса (4.9) следует, что его величина изменяется пропорционально среднему диаметру, а значит отношение qH/rпр постоянно и, следовательно, постоянно контактное напряжение в любом сечении. Поэтому за расчетное принимают среднее сечение зуба. В дополнение к этому, введем коэффициент прочности конических передач
(4.9)
Далее полагаем, что для однопарного зацепления, как было показано ранее, известны нормальная нагрузка qH и приведенный модуль упругости Епр.
Из формулы для приведенного радиуса (4.9) следует, что его величина изменяется пропорционально среднему диаметру, а значит отношение qH/rпр постоянно и, следовательно, постоянно контактное напряжение в любом сечении. Поэтому за расчетное принимают среднее сечение зуба. В дополнение к этому, введем коэффициент прочности конических передач 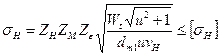 (4.10)
Здесь
(4.10)
Здесь 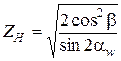 - коэффициент формы сопряженных поверхностей зубьев. Для
- коэффициент формы сопряженных поверхностей зубьев. Для 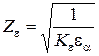 - коэффициент, учитывающий длину контактной линии зацепления конических колес. Обычно
- коэффициент, учитывающий длину контактной линии зацепления конических колес. Обычно 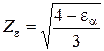 .
.
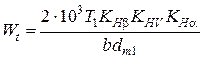 - удельная окружная сила.
Коэффициент
- удельная окружная сила.
Коэффициент 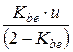 и определяется по графикам на рис.23 в зависимости от конструктивной схемы конической передачи, типа опор колес – Iш (шариковые), Iр (роликовые), а также твердости материала колес.
Здесь:
и определяется по графикам на рис.23 в зависимости от конструктивной схемы конической передачи, типа опор колес – Iш (шариковые), Iр (роликовые), а также твердости материала колес.
Здесь:  Рис. 23. Изменение коэффициентов
Рис. 23. Изменение коэффициентов 
 Коэффициент неравномерности нагрузки зубьев
Коэффициент неравномерности нагрузки зубьев  Обозначив
Обозначив ![clip_image006[8] clip_image006[8]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0068_thumb.gif) , мм. (4.11)
Здесь Кd - вспомогательный коэффициент. Для конических прямозубых передач
, мм. (4.11)
Здесь Кd - вспомогательный коэффициент. Для конических прямозубых передач ![clip_image012[4] clip_image012[4]](https://moscow-stud.com/wp-content/uploads/7eeffbec1d7c_FE9C/clip_image0124_thumb.gif) или
или 