-
Главная
-
Полезные советы
-
Расчет основных статистик и оценка корреляционной связи
Расчет основных статистик и оценка корреляционной связи
В работе необходимо рассчитать основные статистики.
1. Средние величины. В практическом занятии рассчитывается показатель средней арифметической:
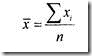
где хi, - значение признака; n - объем совокупности.
2. Размах вариации.
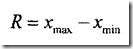
где х
max- максимальное значение признака; х
min - минимальное значение признака.
3. Среднее линейное отклонение.
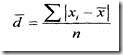
4. Дисперсия признака.
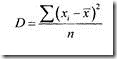
5. Среднее квадратичное отклонение.
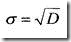
6. Коэффициент вариации.
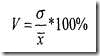
7. Линейный коэффициент корреляции.
Измерение тесноты и направления связи признаков друг с другом является важнейшей задачей статистического исследования социально-экономических явлений. Тесноту и направление связи между признаками можно измерить с помощью линейного коэффициента парной корреляции, который рассчитывается по следующей формуле:
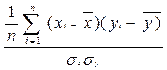
8. Множественный коэффициент корреляции.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками. Для оценки тесноты связи между результативным и двумя факторными признаками множественный коэффициент корреляции рассчитывается по формуле:
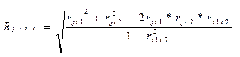
Коэффициент корреляции - это показатель, оценивающий тесноту линейной связи между признаками. Он может принимать значения от -1 до +1. Знак "-" означает, что связь обратная, "+" - прямая. Чем ближе коэффициент к 1 тем теснее линейная связь. Коэффициент =1 означает, что связь между признаками функциональная. Теснота связи оценивается по величине коэффициента корреляции [8]:
если | r | ≤ 0.3 , то связь слабая или совсем отсутствует (необходимы дополнительные исследования статистической значимости коэффициентов);
если 0.3 ≤ | r | ≤ 0.5, связь умеренная;
если 0.5 ≤ | r | ≤ 0.7, значительная;
если 0.7 ≤ | r | ≤ 0.9, тесная;
если > 0.91, очень тесная.
Для практических целей Дворецкий рекомендует использовать значительные, тесные и очень тесные связи.
По величине коэффициента корреляции оцениваем связь между результативными и факторными признаками. Если коэффициент корреляции равен нулю, то линейная связь отсутствует, если коэффициент корреляции положителен, то связь между признаками прямая, если отрицателен, то связь между признаками обратная,
Значение множественного коэффициента корреляции лежит в диапазоне от 0 до 1 и тоже оценивается с помощью приведенных выше диапазонов положительных значений коэффициента корреляции.
9. Нормирование данных.
Нормирование позволяет привести показатели с разной физической сущностью и разными единицами измерения к единому формату в диапазоне от 0 до 1. Нормирование осуществляется путем деления модуля (абсолютной величины) всех членов выборки на максимальную величину данной выборки:
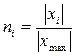
.
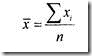 где хi, - значение признака; n - объем совокупности.
где хi, - значение признака; n - объем совокупности.
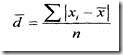
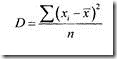
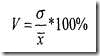
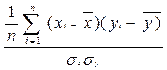
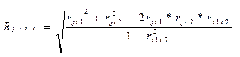 Коэффициент корреляции - это показатель, оценивающий тесноту линейной связи между признаками. Он может принимать значения от -1 до +1. Знак "-" означает, что связь обратная, "+" - прямая. Чем ближе коэффициент к 1 тем теснее линейная связь. Коэффициент =1 означает, что связь между признаками функциональная. Теснота связи оценивается по величине коэффициента корреляции [8]:
если | r | ≤ 0.3 , то связь слабая или совсем отсутствует (необходимы дополнительные исследования статистической значимости коэффициентов);
если 0.3 ≤ | r | ≤ 0.5, связь умеренная;
если 0.5 ≤ | r | ≤ 0.7, значительная;
если 0.7 ≤ | r | ≤ 0.9, тесная;
если > 0.91, очень тесная.
Для практических целей Дворецкий рекомендует использовать значительные, тесные и очень тесные связи.
По величине коэффициента корреляции оцениваем связь между результативными и факторными признаками. Если коэффициент корреляции равен нулю, то линейная связь отсутствует, если коэффициент корреляции положителен, то связь между признаками прямая, если отрицателен, то связь между признаками обратная,
Значение множественного коэффициента корреляции лежит в диапазоне от 0 до 1 и тоже оценивается с помощью приведенных выше диапазонов положительных значений коэффициента корреляции.
Коэффициент корреляции - это показатель, оценивающий тесноту линейной связи между признаками. Он может принимать значения от -1 до +1. Знак "-" означает, что связь обратная, "+" - прямая. Чем ближе коэффициент к 1 тем теснее линейная связь. Коэффициент =1 означает, что связь между признаками функциональная. Теснота связи оценивается по величине коэффициента корреляции [8]:
если | r | ≤ 0.3 , то связь слабая или совсем отсутствует (необходимы дополнительные исследования статистической значимости коэффициентов);
если 0.3 ≤ | r | ≤ 0.5, связь умеренная;
если 0.5 ≤ | r | ≤ 0.7, значительная;
если 0.7 ≤ | r | ≤ 0.9, тесная;
если > 0.91, очень тесная.
Для практических целей Дворецкий рекомендует использовать значительные, тесные и очень тесные связи.
По величине коэффициента корреляции оцениваем связь между результативными и факторными признаками. Если коэффициент корреляции равен нулю, то линейная связь отсутствует, если коэффициент корреляции положителен, то связь между признаками прямая, если отрицателен, то связь между признаками обратная,
Значение множественного коэффициента корреляции лежит в диапазоне от 0 до 1 и тоже оценивается с помощью приведенных выше диапазонов положительных значений коэффициента корреляции.
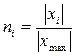 .
.
