-
Главная
-
Полезные советы
-
Расчет зубчатой передачи на прочность
Расчет зубчатой передачи на прочность
Впервые контактную задачу сформулировал и решил Г. Герц (Herz), рассмотрев сжатие двух цилиндров под действием распределенной нагрузки
q (Рис. 8).
Первоначальный контакт осуществляется по линии
у-у. При сжатии цилиндров распределенной по длине
l нагрузкой
q в результате упругой деформации образуется площадка контакта в виде прямоугольника шириной 2
а.
Наибольшее напряжение на поверхности контакта
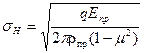
, МПа. (2.1)
Формула справедлива при условии следующих допущений:
1. Действующие усилия направлены нормально к поверхности соприкосновения цилиндров.
2. Нагрузка распределена равномерно по поверхности контактирующих цилиндров
q = const.
3. Силы трения отсутствуют.
4. Материалы соприкасающихся тел однородны и изотропны.
5. Поверхности абсолютно гладкие.
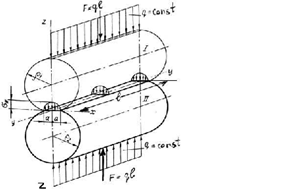
Рис.8
В формуле (2.1)
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/c9be533c63e4_C637/clip_image0026_thumb.gif)
МПа – приведенный модуль упругости, а Е
1 и Е
2 – модули упругости материала цилиндров,
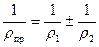
- приведенный радиус кривизны, μ – коэффициент Пуассона материала цилиндров (для большинства стальных зубчатых колес принимается μ=0,3).
Расчет зубчатой передачи на контактную выносливость
Наибольшие контактные напряжения возникают в тонком поверхностном слое материала. Толщина этого слоя составляет (0,2…0,5) мм.
В качестве исходной зависимости, принимают формулу Герца (2.1)
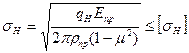
,
где
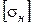
- допускаемое контактное напряжение, зависящее от материала колес, химико-термической обработки и технологии изготовления зубчатого колеса;
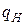
– расчетная нормальная погонная нагрузка,
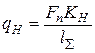
Н/мм.
Подставляя из формул (1.1) и (1.2) (см. лекцию 1) выражения для величин
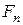
и
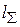
, получим:
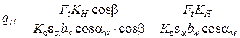
, или
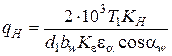
Н/мм, (2.2),
где
КН – коэффициент нагрузки.
Если испытываете трудности в написании
контрольной работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
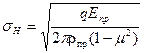 , МПа. (2.1)
Формула справедлива при условии следующих допущений:
1. Действующие усилия направлены нормально к поверхности соприкосновения цилиндров.
2. Нагрузка распределена равномерно по поверхности контактирующих цилиндров q = const.
3. Силы трения отсутствуют.
4. Материалы соприкасающихся тел однородны и изотропны.
5. Поверхности абсолютно гладкие.
, МПа. (2.1)
Формула справедлива при условии следующих допущений:
1. Действующие усилия направлены нормально к поверхности соприкосновения цилиндров.
2. Нагрузка распределена равномерно по поверхности контактирующих цилиндров q = const.
3. Силы трения отсутствуют.
4. Материалы соприкасающихся тел однородны и изотропны.
5. Поверхности абсолютно гладкие.
 Рис.8
В формуле (2.1)
Рис.8
В формуле (2.1) 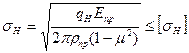 ,
где
,
где 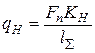 Н/мм.
Подставляя из формул (1.1) и (1.2) (см. лекцию 1) выражения для величин
Н/мм.
Подставляя из формул (1.1) и (1.2) (см. лекцию 1) выражения для величин 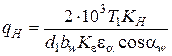 Н/мм, (2.2),
где КН – коэффициент нагрузки.
Если испытываете трудности в написании контрольной работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
Н/мм, (2.2),
где КН – коэффициент нагрузки.
Если испытываете трудности в написании контрольной работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
