-
Главная
-
Полезные советы
-
Расчет зубчатой передачи на изгибную выносливость
Расчет зубчатой передачи на изгибную выносливость
Поломка зубьев является самым опасным видом повреждения, приводящим к выходу из строя передачи и других деталей (валов, подшипников). Это происходит в результате перегрузок ударного или статического действия (пиковых) или усталостного изгиба, вызванного многократно повторяющимися нагрузками, превышающими предел выносливости материала зубьев, т.е. в результате усталости материала.
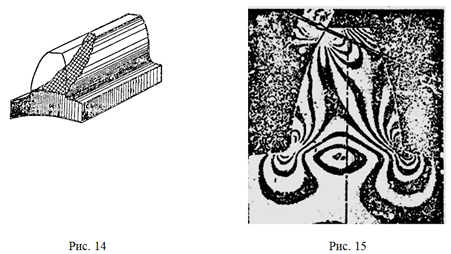
Зубья косозубых колес выламываются по косому сечению от вершины до основания (см. рисунок 14). При усталостном разрушении излом имеет вогнутую форму на поверхности колеса, а при перегрузках – выпуклую.
 Предпосылки к расчету на изгибную выносливость
Предпосылки к расчету на изгибную выносливость
1. Сила нормального давления приложена к вершине зуба (рис. 15).
2. В зацеплении участвует одна пара зубьев.
3. Пренебрегаем силами трения.
4. Моделируем зуб консольной балкой.
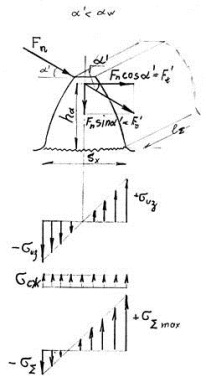
Рис. 16.
Как видно из рисунка 16, сила
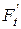
, действующая под углом
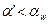
, (с целью увеличения запаса прочности) вызывает напряжение изгиба зуба, а сила
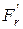
- сжатие.
Известно, что напряжение изгиба
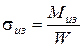
, где
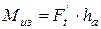
,
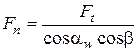
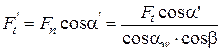
(см. рис 16). Таким образом
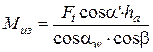
. Момент сопротивления сечения
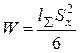
. Подставляя, в исходное уравнение, получим:
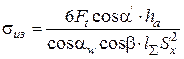
,
где
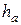
- плечо силы
![clip_image002[1] clip_image002[1]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0021_thumb.gif)
,
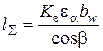
- суммарное число контактных зубьев в зацеплении.
Напряжение сжатия
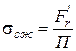
,
где
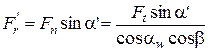
,
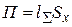
.
Подставив, найдем:
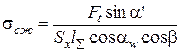
.
Из эпюр (рис. 16) следует, что критическая сторона левая, растянутая, поэтому
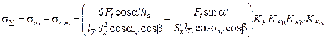
,
где –
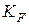
- коэффициент влияния силы сдвига по поверхности зуба и концентрации напряжений у основания зуба;
KFb - коэффициент концентрации давления при изгибе зуба, учитывающий неравномерность распределения давления по длине зуба, определяется аналогично с расчетом на контактную прочность по рисунку 17;
KFV – коэффициент динамичности нагрузки, прикладываемой к зубу при изгибе, находится по таблице 3 (лекция 2);
KFa - коэффициент неравномерности распределения нагрузки между зубьями в случае в многопарного зацепления; определяется по таблице 4 (лекция 2).
Так как размер зубьев пропорционален модулю
m, принимаем
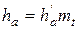
;
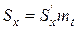
, где
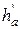
и
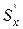
- коэффициенты пропорциональности. Подставляя эти значения коэффициентов, получим при
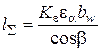
критическое значение напряжения:
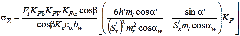
.
Обозначим выражение в квадратных скобках через
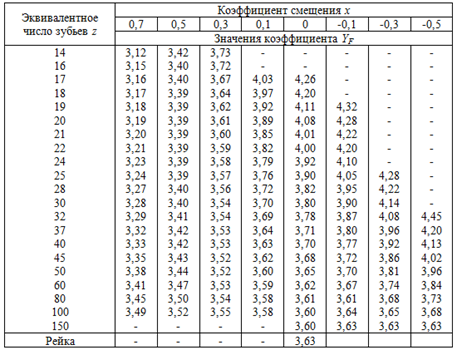
YF - параметр, называемый коэффициентом формы зуба. Он определяется из таблицы 6, в зависимости от эквивалентного числа зубьев
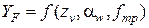
, где
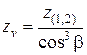
.
Окончательно
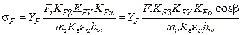
.
Введем обозначение
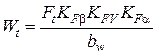 Проверка расчета на изгибную выносливость
Проверка расчета на изгибную выносливость
получаем уравнение:
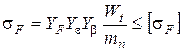
, (3.2)
Здесь:
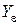
- коэффициент перекрытия зубьев
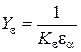
; коэффициент, учитывающий наклон зубьев,
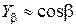
или
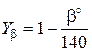
.
При изменении β = 0…42
о Yb изменяется от 1,0 до 0,7, то есть, с увеличением β прямо пропорционально уменьшается.
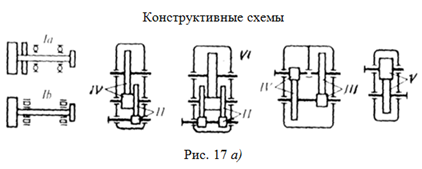
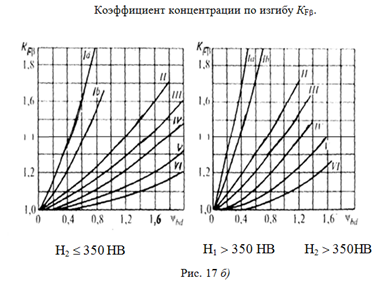
В другой форме уравнение (3.2) запишется так:
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0028_thumb.gif)
,
или так
![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0046_thumb.gif)
. (3.3).
Условие равной прочности зубьев шестерни и колеса на изгиб таково:
![clip_image006[6] clip_image006[6]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0066_thumb.gif)
(3.4)
Отношение
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0084_thumb.gif)
следует брать меньшее для шестерни или колеса.
Таблица 7.
Коэффициент формы зуба YF
Проверка изгибной прочности зубьев при перегрузке
![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image00210_thumb.gif)
(3.5).
Если испытываете трудности в написании
курсовой работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
 Предпосылки к расчету на изгибную выносливость
1. Сила нормального давления приложена к вершине зуба (рис. 15).
2. В зацеплении участвует одна пара зубьев.
3. Пренебрегаем силами трения.
4. Моделируем зуб консольной балкой.
Предпосылки к расчету на изгибную выносливость
1. Сила нормального давления приложена к вершине зуба (рис. 15).
2. В зацеплении участвует одна пара зубьев.
3. Пренебрегаем силами трения.
4. Моделируем зуб консольной балкой.
 Рис. 16.
Как видно из рисунка 16, сила
Рис. 16.
Как видно из рисунка 16, сила 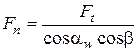
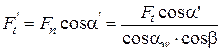 (см. рис 16). Таким образом
(см. рис 16). Таким образом 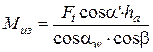 . Момент сопротивления сечения
. Момент сопротивления сечения 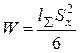 . Подставляя, в исходное уравнение, получим:
. Подставляя, в исходное уравнение, получим:
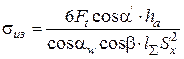 ,
где
,
где 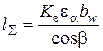 - суммарное число контактных зубьев в зацеплении.
Напряжение сжатия
- суммарное число контактных зубьев в зацеплении.
Напряжение сжатия 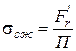 ,
где
,
где 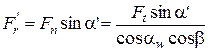 ,
, 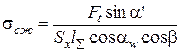 .
Из эпюр (рис. 16) следует, что критическая сторона левая, растянутая, поэтому
.
Из эпюр (рис. 16) следует, что критическая сторона левая, растянутая, поэтому 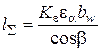 критическое значение напряжения:
критическое значение напряжения:
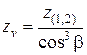 .
Окончательно
.
Окончательно 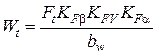 Проверка расчета на изгибную выносливость
получаем уравнение:
Проверка расчета на изгибную выносливость
получаем уравнение:
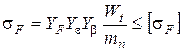 , (3.2)
Здесь:
, (3.2)
Здесь: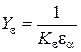 ; коэффициент, учитывающий наклон зубьев,
; коэффициент, учитывающий наклон зубьев, 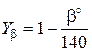 .
При изменении β = 0…42о Yb изменяется от 1,0 до 0,7, то есть, с увеличением β прямо пропорционально уменьшается.
.
При изменении β = 0…42о Yb изменяется от 1,0 до 0,7, то есть, с увеличением β прямо пропорционально уменьшается.

 В другой форме уравнение (3.2) запишется так:
В другой форме уравнение (3.2) запишется так:
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0028_thumb.gif) ,
или так
,
или так
![clip_image004[6] clip_image004[6]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0046_thumb.gif) . (3.3).
Условие равной прочности зубьев шестерни и колеса на изгиб таково:
. (3.3).
Условие равной прочности зубьев шестерни и колеса на изгиб таково:
![clip_image006[6] clip_image006[6]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image0066_thumb.gif) (3.4)
Отношение
(3.4)
Отношение  Проверка изгибной прочности зубьев при перегрузке
Проверка изгибной прочности зубьев при перегрузке
![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/93ec813f6f9b_DCA9/clip_image00210_thumb.gif) (3.5).
Если испытываете трудности в написании курсовой работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
(3.5).
Если испытываете трудности в написании курсовой работы по деталям машин, оформите заявку и Вы узнаете сроки и стоимость работы.
