-
Главная
-
Полезные советы
-
Решение задач на плоскую систему сил.
Решение задач на плоскую систему сил.
Пример (рис.1.30). Определить реакции шарнирно опертой балки, нагруженной силой
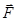
и парой сил с моментом М.
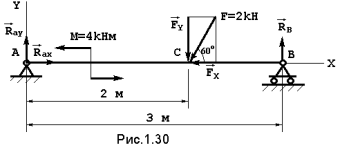
Решение. Воспользуемся тем же планом, который применялся для решения задач на сходящуюся систему сил. Объектом равновесия является вся балка, нагрузка на которую показана на чертеже. Отбросим связи - шарниры А и В. Реакцию неподвижного шарнира А разложим на две составляющих -
![clip_image002[5] clip_image002[5]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image0025_thumb.png)
и
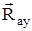
, а реакция подвижного шарнира В направлена перпендикулярно опорной плоскости. Таким образом, на балку действует плоская произвольная система сил, для которой можно составить три уравнения равновесия. Выберем оси координат и составим эти уравнения. Уравнения проекций:
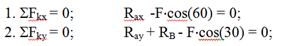
(пара в уравнение проекций не входит, так как сумма проекций сил пары на любую ось равна нулю).
Уравнение моментов составляем относительно точки А, поскольку в ней пересекаются две неизвестных силы. При нахождении момента пары относительно точки А помним, что сумма моментов сил пары относительно любой точки равен моменту пары, а знак момента будет положительным, поскольку пара стремится повернуть тело против часовой стрелки. Для нахождения момента силы
![clip_image002[7] clip_image002[7]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image0027_thumb.png)
удобно разложить ее на вертикальную и горизонтальную составляющие:
F
x=Fcos(60), F
y=Fcos(30)
и воспользоваться теоремой Вариньона, причем следует учесть, что момент от силы
![clip_image002[9] clip_image002[9]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image0029_thumb.png)
относительно точки А равен нулю, поскольку ее линия действия проходит через эту точку. Тогда уравнение моментов примет вид:
3.
![clip_image002[11] clip_image002[11]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image00211_thumb.png)
; R
в.3-F
B×cos(30)×2 + M = 0.
Решая это уравнение получим:
![clip_image002[13] clip_image002[13]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image00213_thumb.png)
Из уравнения (2) находим:
R
ay = F×cos(30) - R
B = 2×0,867 - 4=-2,67 кН, а из уравнения (1) R
ax = F×cos(60) = 2×0,5 = 1 кН.
Пример (рис.1.31). Определить реакции жестко защемленной балки длиной 3 м, нагруженной равномерно распределенной нагрузкой итенсивностью q=10кН/м.
![clip_image001[6] clip_image001[6]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image0016_thumb.png)
Решение. Заменим равномерно распределенную нагрузку ее равнодействующей Q= 3×q = 3×10 = 30 кН. Она будет приложена в середине пролета, то есть на расстоянии АС = 1,5 м. Рассматриваем равновесие балки АВ. Отбрасываем связь - жесткую заделку, а вместо нее прикладываем две составляющие реакции R
ах и R
ау и реактивный момент M
а. На балку будет действовать плоская произвольная система сил, для которой можно составить три уравнения равновесия, из которых можно найти искомые неизвестные.
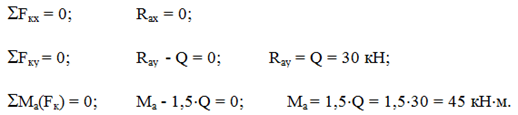
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
 Решение. Воспользуемся тем же планом, который применялся для решения задач на сходящуюся систему сил. Объектом равновесия является вся балка, нагрузка на которую показана на чертеже. Отбросим связи - шарниры А и В. Реакцию неподвижного шарнира А разложим на две составляющих -
Решение. Воспользуемся тем же планом, который применялся для решения задач на сходящуюся систему сил. Объектом равновесия является вся балка, нагрузка на которую показана на чертеже. Отбросим связи - шарниры А и В. Реакцию неподвижного шарнира А разложим на две составляющих - ![clip_image001[6] clip_image001[6]](https://moscow-stud.com/wp-content/uploads/4afc67dab74f_CF12/clip_image0016_thumb.png) Решение. Заменим равномерно распределенную нагрузку ее равнодействующей Q= 3×q = 3×10 = 30 кН. Она будет приложена в середине пролета, то есть на расстоянии АС = 1,5 м. Рассматриваем равновесие балки АВ. Отбрасываем связь - жесткую заделку, а вместо нее прикладываем две составляющие реакции Rах и Rау и реактивный момент Mа. На балку будет действовать плоская произвольная система сил, для которой можно составить три уравнения равновесия, из которых можно найти искомые неизвестные.
Решение. Заменим равномерно распределенную нагрузку ее равнодействующей Q= 3×q = 3×10 = 30 кН. Она будет приложена в середине пролета, то есть на расстоянии АС = 1,5 м. Рассматриваем равновесие балки АВ. Отбрасываем связь - жесткую заделку, а вместо нее прикладываем две составляющие реакции Rах и Rау и реактивный момент Mа. На балку будет действовать плоская произвольная система сил, для которой можно составить три уравнения равновесия, из которых можно найти искомые неизвестные.
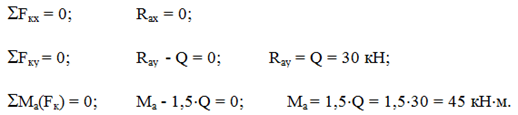 Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
