-
Главная
-
Полезные советы
-
Сферическое движение в кинематике.
Сферическое движение в кинематике.
Сферическое движение – движение твердого тела, одна из точек которого во все время движения остается неподвижной (например движение волчка).
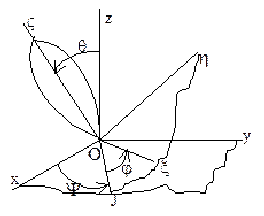
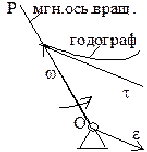
Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f
1(t); q=f
2(t); j=f
3(t). Углы отсчитываются от осей против хода часовой стрелки.
Теорема Эйлера-Даламбера.
Всякое перемещение тела, имеющего неподвижную точку, можно заменить одним поворотом вокруг некоторой мгновенной оси вращения, проходящей через эту точку. Скорости всех точек тела, лежащих на мгновенной оси вращения в данный момент времени равны нулю. Вектор угловой скорости (мгновенной угловой скорости) откладывается о неподвижной точки по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение происходящим против часовой стрелки. Вектор угловой скорости со временем изменяется не только по численной величине, но и по направлению. Конец вектора описывает годограф скорости вектора
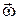
Угловое ускорение:
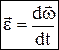
– скорость конца вектора
![clip_image006[1] clip_image006[1]](https://moscow-stud.com/wp-content/uploads/bb007a3b46ce_C7D1/clip_image0061_thumb.gif)
, совпадает по направлению с касательной к годографу вектора угловой скорости. В случае сферического движения в отличии от случая вращения вокруг неподвижной оси вектор
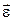
не совпадает с направлением
![clip_image006[2] clip_image006[2]](https://moscow-stud.com/wp-content/uploads/bb007a3b46ce_C7D1/clip_image0062_thumb.gif)
. Скорости точек при сферическом движении:
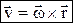
– векторное произведение,
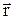
– радиус-вектор точки, проведенный из неподвижной точки, модуль v=wr×sina=w×h, h– расстояние от точки до мгновенной оси вращения.
Формулы Эйлера:
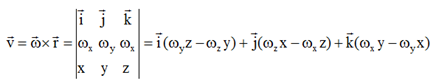
.
Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
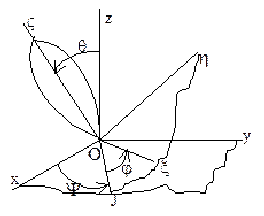
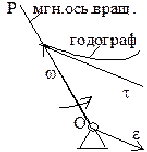 Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Углы отсчитываются от осей против хода часовой стрелки.
Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Углы отсчитываются от осей против хода часовой стрелки.
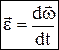 – скорость конца вектора
– скорость конца вектора 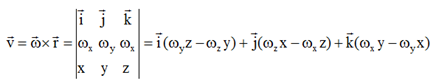 .
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
.
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
