-
Главная
-
Полезные советы
-
Силовое поле в динамике.
Силовое поле в динамике.
Силовое поле – область, в каждой точке которой на помещенную в ней материальную точку действует сила, однозначно определенная по величине и направлению в любой момент времени, т.е. должно быть известна
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/dbefecf817a5_D8FC/clip_image0024_thumb.gif)
. Нестационарное силовое поле, если
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/dbefecf817a5_D8FC/clip_image0044_thumb.gif)
явно зависит от t, стационарное силовое поле, если сила не зависит от времени. Рассматриваются стационарные силовые поля, когда сила зависит только от положения точки:
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/dbefecf817a5_D8FC/clip_image0064_thumb.gif)
и F
x=F
x(x,y,z) и т.д.
Свойства стационарных силовых полей:
1) Работа сил стационарного поля зависит в общем случае от начального М
1 и конечного М
2 положений и траектории, но не зависит от закона движения материальной точки.
2) Имеет место равенство А
2,1= – А
1,2. Для нестационарных полей эти свойства на выполняются.
Примеры: поле силы тяжести, электростатическое поле, поле силы упругости.
Стационарные силовые поля, работа сил которых не зависит от траектории (пути) движения матер. точки и определяется только ее начальным и конечным положениями называется потенциальными (консервативными).
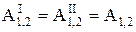
, где I и II – любые пути, А
1,2 – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так:
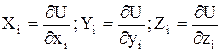
.
Функция U=U(x
1,y
1,z
1,x
2,y
2,z
2,…x
n,y
n,z
n) называется силовой функцией. Элементарная работа сил поля: dА=ådА
i= dU. Если силовое поле является потенциальным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции.
Работа сил на конечном перемещении
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/dbefecf817a5_D8FC/clip_image0026_thumb.gif)
, т.е. работа сил в потенциальном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П
0= 0. П=П(x
1,y
1,z
1,x
2,y
2,z
2,…x
n,y
n,z
n). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А
1,2= П
1– П
2.
Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U
0: А
1,0= П =U
0 – U. Потенциальная энергия поля силы тяжести: П= mgz.
Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра:
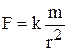
,
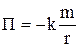
.
Центральной является гравитационная сила
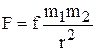
,
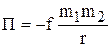
, f = 6,67×10
-11м
3/(кгс
2) – постоянная тяготения.
Первая космическая скорость v
1=
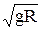
» 7,9 км/с, R = 6,37×10
6м – радиус Земли; тело выходит на круговую орбиту.
Вторая космическая скорость: v
11=
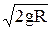
» 11,2 км/с, траектория тела парабола, при v >v
11– гипербола.
Потенциальная энергия восстанавливающей силы пружин:
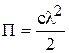
, l – модуль приращения длины пружины.
Работа восстанавливающей силы пружины:
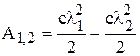
, l
1 и l
2 – деформации, соответствующие начальной и конечной точкам пути.
Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
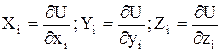 .
Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn) называется силовой функцией. Элементарная работа сил поля: dА=ådАi= dU. Если силовое поле является потенциальным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции.
Работа сил на конечном перемещении
.
Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn) называется силовой функцией. Элементарная работа сил поля: dА=ådАi= dU. Если силовое поле является потенциальным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции.
Работа сил на конечном перемещении ![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/dbefecf817a5_D8FC/clip_image0026_thumb.gif) , т.е. работа сил в потенциальном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П0= 0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А1,2= П1– П2.
Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: П= mgz.
Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра:
, т.е. работа сил в потенциальном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П0= 0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А1,2= П1– П2.
Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: П= mgz.
Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра: 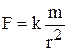 ,
, 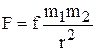 ,
, 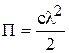 , l – модуль приращения длины пружины.
Работа восстанавливающей силы пружины:
, l – модуль приращения длины пружины.
Работа восстанавливающей силы пружины: 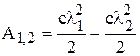 , l1 и l2 – деформации, соответствующие начальной и конечной точкам пути.
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
, l1 и l2 – деформации, соответствующие начальной и конечной точкам пути.
Если испытываете трудности в написании курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
