-
Главная
-
Полезные советы
-
Скорость и ускорение точки.
Скорость и ускорение точки.
Скорость точки:
Вектор скорости:
![clip_image002[12] clip_image002[12]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00212_thumb.gif)
– первая производная от радиус-вектора по времени (точка обозначает производную по времени);
![clip_image002[14] clip_image002[14]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00214_thumb.gif)
.
Проекции скорости:
![clip_image002[16] clip_image002[16]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00216_thumb.gif)
,
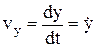
,
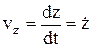
.
Модуль скорости:
![clip_image002[18] clip_image002[18]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00218_thumb.gif)
, направляющие косинусы:
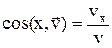
и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным. При естественном способе:
![clip_image002[20] clip_image002[20]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00220_thumb.gif)
– модуль скорости, вектор скорости:
![clip_image002[22] clip_image002[22]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00222_thumb.gif)
,
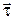
– орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление
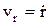
, поперечное направление
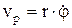
, модуль скорости
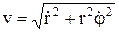
; x=rcosj, y=rsinj.
Ускорение точки
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image0028_thumb.gif)
, [м/сек
2].
Проекции ускорения
![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00210_thumb.gif)
т.д.
Модуль ускорения:
![clip_image002[24] clip_image002[24]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00224_thumb.gif)
направляющие косинусы:
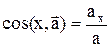
, и т.д.
При задании движения в полярных координатах: проекции ускорения на радиальное направление
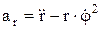
, поперечное направление
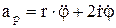
, модуль ускорения
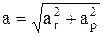
. При естественным способе задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:
![clip_image002[26] clip_image002[26]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00226_thumb.gif)
. Модуль нормального ускорения:
![clip_image002[28] clip_image002[28]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00228_thumb.gif)
, r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (
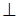
к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения
![clip_image002[30] clip_image002[30]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00230_thumb.gif)
, направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движении направление касательного ускорения и скорости совпадают, при замедленном – противоположно.
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image0044_thumb.gif)
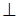
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image0064_thumb.gif)
, следовательно
![clip_image002[32] clip_image002[32]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00232_thumb.gif)
. Вектор ускорения лежит в соприкасающейся плоскости, следовательно его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль –
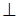
к главной нормали и касательной).
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
![clip_image002[8] clip_image002[8]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image0028_thumb.gif) , [м/сек2].
Проекции ускорения
, [м/сек2].
Проекции ускорения ![clip_image002[28] clip_image002[28]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00228_thumb.gif) , r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (
, r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (![clip_image002[30] clip_image002[30]](https://moscow-stud.com/wp-content/uploads/547171694c52_DC61/clip_image00230_thumb.gif) , направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движении направление касательного ускорения и скорости совпадают, при замедленном – противоположно.
, направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движении направление касательного ускорения и скорости совпадают, при замедленном – противоположно. 