1. Главная
2. Полезные советы
3. Составьте распределение числа прибывших машин.

Составьте распределение числа прибывших машин.

Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго - 0,3, от третьего - 0,1.

Необходимо:

1. Составить распределение числа прибывших машин.

2. Найти математическое ожидание и дисперсию полученной случайной величины.

3. Построить график интегральной функции распределения.

Решение:

Очевидно, что случайная величина X - число прибывших машин может принимать четыре возможных значения - 0, 1, 2, 3. Найдем вероятности этих событий: P(X = 0) = 0,8 • 0,7 • 0,9 = 0,504, P(X = 1) = 0,2 • 0,7 • 0,9 + 0,8 • 0,3 • 0,9 + 0,8 • 0,7 • 0,1 = 0,398, P(X = 2) = 0,2 • 0,3 • 0,9 + 0,2 • 0,7 • 0,1 + 0,8 • 0,3 • 0,1 = 0,092, P(X = 3) = 0,2 • 0,3 • 0,1 = 0,006. Закон распределения дискретной случайной величины X - числа прибывших машин имеет вид:

x,	0	1	2	3
p, = P(X = x)	0,504	0,398	0,092	0,006

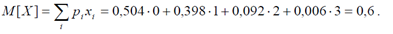
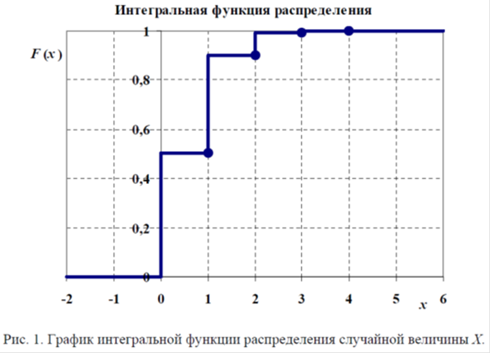
Математическое ожидание случайной величины равно Дисперсия равна: D[X] = M[X²] - M[X]² = ∑x_i²p_i - ∑ x_ip_i . M[X²] = 0² • 0,504 +1² • 0,398 + 2² • 0,092 + 3² • 0,006 = 0,82. D[X] = 0,82 - 0,6² = 0,82 - 0,36 = 0,46 . График интегральной функции распределения случайной величины X, приведен на рис. 1. Рис. 1. График интегральной функции распределения случайной величины X. Если испытываете трудности в написании курсовой работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.