-
Главная
-
Полезные советы
-
Статическая неопределимость задачи сопротивления материалов.
Статическая неопределимость задачи сопротивления материалов.
Рассмотрим поперечное сечение бруса (рис. 3.2).
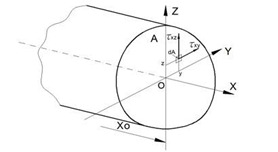
Рис. 3.2 Иллюстрация к записи выражений (3.1)
На малой площадке этого сечения dA действуют нормальные σ
x и касательные τ
xy и τ
xz напряжения.
Учитывая, что главный вектор и главный момент внутренних сил в сечении статически эквивалентны системе напряжений в нём, запишем их компоненты относительно главных центральных осей OX, OY и OZ., проинтегрировав элементарные силы и моменты, создаваемые напряжениями на площадке dA:
N
x =
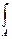
σ
xdA ; Q
y =
![clip_image004[1] clip_image004[1]](https://moscow-stud.com/wp-content/uploads/9a07d539e1ff_C5F5/clip_image0041_thumb.gif)
τ
xydA ; Q
z =
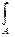
τ
xzdA ;
(3.1)
M
x =
![clip_image004[2] clip_image004[2]](https://moscow-stud.com/wp-content/uploads/9a07d539e1ff_C5F5/clip_image0042_thumb.gif)
(zτ
xy- yτ
xz )dA ; M
y =
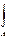
zσ
xdA ; M
z =
![clip_image009[1] clip_image009[1]](https://moscow-stud.com/wp-content/uploads/9a07d539e1ff_C5F5/clip_image0091_thumb.gif)
yσ
xdA.
Подынтегральные функции в правой части выражений (3.1)
σ
x = σ
x(x
0,y,z); τ
xy = τ
xz(x
0,y,z); τ
xz = τ
xz(x
0,y,z), (3.2)
где x
0 абсцисса сечения, не могут быть однозначно определены по заданному внутреннему силовому фактору слева. То есть уравнений равновесия статики (2.1), (2.2), (3.1) недостаточно для нахождения законов распределения внутренних сил в поперечном сечении бруса. Этот факт носит название статическая неопределимость задачи сопротивления материалов.
Следовательно, для определения напряжений и деформаций (раскрытия статической неопределимости) необходимо составить дополнительные уравнения, рассмотрев кроме статической стороны задачи другие её стороны:
-перемещения и деформации в рамках ограничений, которые на них накладывает гипотеза плоских сечений;
-связь напряжений с деформациями, обусловленную законом Гука.
Если испытываете трудности в написании
контрольной работы по сопротивлению материалов, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
 Рис. 3.2 Иллюстрация к записи выражений (3.1)
На малой площадке этого сечения dA действуют нормальные σx и касательные τxy и τxz напряжения.
Учитывая, что главный вектор и главный момент внутренних сил в сечении статически эквивалентны системе напряжений в нём, запишем их компоненты относительно главных центральных осей OX, OY и OZ., проинтегрировав элементарные силы и моменты, создаваемые напряжениями на площадке dA:
Nx =
Рис. 3.2 Иллюстрация к записи выражений (3.1)
На малой площадке этого сечения dA действуют нормальные σx и касательные τxy и τxz напряжения.
Учитывая, что главный вектор и главный момент внутренних сил в сечении статически эквивалентны системе напряжений в нём, запишем их компоненты относительно главных центральных осей OX, OY и OZ., проинтегрировав элементарные силы и моменты, создаваемые напряжениями на площадке dA:
Nx =