-
Главная
-
Полезные советы
-
Статистический анализ вариационных (интервальных) данных
Статистический анализ вариационных (интервальных) данных
Совокупность значений изучаемого признака с указанием числа их различных значений называется распределением признака. Распределение представляют в форме вариационного ряда. В соотношении значений признака (вариантов) и числа единиц (частот) проявляется закономерность распределения. Она описывается различными статистическими показателями в частности:
· частотные показатели;
· показатели центра распределения;
· показатели степени вариации;
· показатели формы распределения.
Частотными показателями
любого ряда распределения являются абсолютная численность i- и группы — частота f
iи относительная частота — частость d
i, где
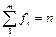
, а
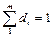
, или 100%.
Кумулятивная (накопленная) частота S
i (частость S
d) характеризует объем совокупности со значениями вариантов, не превышающих X
i,. Кумулятивные частотные показатели образуются последовательным суммированием абсолютных или относительных частот, например:
S1=fi; S2=f1+f2; S3=f1+f2+f3 и т. д.
Плотность частоты (частости) представляет собой частоту, приходящуюся на единицу интервала, т.е.
qi=fi/hiили
qi=di/hi, где
hi, - величина
i-го интервала. Данный показатель используют, если интервалы вариационного ряда неравные и необходимо графически изобразить этот ряд в виде гистограммы, а так же при расчете моды.
Показатели центра распределения. К показателям центра распределения относят
среднюю, моду и медиану.
Средняя величина характеризует типичный уровень признака в совокупности. По данным вариационного ряда распределения средняя рассчитывается как арифметическая взвешенная:
· на основе частот:
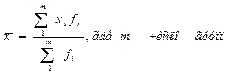
· на основе частостей
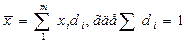
Если используется интервальный ряд распределения то, допуская, что распределение в границах
i-го интервала является равномерным, как вариант х
i, - используют середину интервала (
х'). При этом величину открытого интервала условно считают такой же, как и величину соседнего закрытого интервала.
Пример. Провести анализ данных о результатах деятельности предприятия по оказанию услуг. В таблице 5.1 приводится данные о частоте с которой встречается дневная реализация в соответствующем диапазоне.
Таблица 5.1
Результаты деятельности предприятии по оказанию услуг населению
| Возраст оборудования, тас.руб |
Количество дней (fi) |
Середина интервала хi |
хifi |
Накопленная частота, Si |
[xi-xср] |
[xi-xср]*fi |
[xi-xср]2 *fi |
(xi-xср)3 *fi |
(xi-xср)4 *fi |
| До 5 |
10 |
2,5 |
25 |
10 |
11,2 |
112,0 |
1254,4 |
-14049 |
157351 |
| 5 – 10 |
19 |
7,5 |
142,5 |
29 |
6,2 |
117,8 |
730,4 |
-4528,2 |
28075 |
| 10 – 15 |
30 |
12,5 |
375 |
59 |
1,2 |
36,0 |
43,2 |
-51,8 |
62,2 |
| 15 – 20 |
24 |
17,5 |
420 |
83 |
3,8 |
91,2 |
346,6 |
1316,9 |
5004,3 |
| 20 - 25 |
12 |
22,5 |
270 |
95 |
8,8 |
105,6 |
929,3 |
8177,7 |
71963,4 |
| 25 - 30 |
5 |
27,5 |
137,5 |
100 |
13,8 |
69,0 |
952,2 |
13140 |
181337 |
| å |
100 |
- |
1370 |
|
|
531,6 |
4256,0 |
4005,6 |
443793 |
Внимание! В контрольных заданиях, исходные данные могут задаваться в виде величины дневной реализации, см. табл. 5.2 и рис. 5.1. В этом случае необходимо преобразовать исходные данные в частотные. Для этого необходимо провести группировку (см. выше) исходных данных с равными группировочными интервалами. В ниже приведенном примере, интервал принимается равным 0,4 тыс. руб., а весь диапазон разбивается на 10 групп (то есть необходимо сощитать количество дней, в которые реализация находилась в заданных границах).
Таблица 5.2
Динамика оказание услуг по четырем месяцам, тыс.руб.
| День |
№ декады |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
8 |
10 |
11 |
12 |
| 1 |
5,29 |
4,86 |
4,60 |
5,07 |
4,58 |
4,22 |
5,22 |
5,01 |
5,34 |
5,76 |
5,97 |
4,40 |
| 2 |
5,66 |
5,88 |
4,79 |
4,78 |
4,40 |
5,47 |
4,80 |
4,40 |
4,82 |
4,75 |
5,27 |
5,31 |
| 3 |
4,80 |
4,15 |
4,70 |
4,95 |
5,05 |
4,49 |
4,63 |
4,73 |
5,10 |
4,81 |
4,27 |
5,58 |
| 4 |
5,52 |
5,67 |
5,03 |
5,44 |
4,82 |
4,93 |
4,83 |
4,76 |
5,27 |
4,30 |
5,64 |
5,79 |
| 5 |
5,89 |
6,16 |
4,05 |
5,18 |
4,78 |
5,36 |
4,86 |
4,89 |
5,32 |
5,39 |
4,68 |
4,75 |
| 6 |
6,03 |
4,41 |
5,68 |
5,33 |
5,07 |
5,23 |
4,35 |
5,24 |
4,99 |
4,12 |
4,47 |
5,49 |
| 7 |
5,11 |
5,67 |
4,39 |
4,86 |
5,19 |
5,01 |
5,80 |
5,09 |
5,61 |
5,25 |
5,13 |
5,56 |
| 8 |
4,35 |
5,22 |
4,81 |
5,41 |
5,80 |
4,91 |
4,52 |
4,51 |
5,13 |
4,95 |
4,85 |
6,24 |
| 9 |
4,57 |
4,99 |
4,96 |
4,96 |
4,75 |
5,19 |
5,21 |
4,19 |
5,12 |
4,92 |
5,23 |
4,79 |
| 10 |
5,22 |
5,34 |
4,27 |
5,08 |
4,12 |
5,52 |
5,47 |
5,18 |
4,61 |
5,42 |
4,53 |
4,97 |
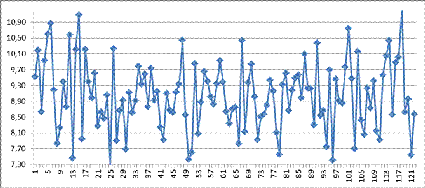
Рис. 5.1 Динамика продаж услуги, тыс.руб.
В результате исходные данные преобразуются в частотный вид см. табл. 5.3.
Таблица 5.3
Частотная интерпретация исходных данных
| Возраст оборудования, тыс.руб |
Количество дней (fi) |
Середина интервала хi |
| 7,3 – 7,7 |
8 |
7,5 |
| 7,7 -8,1 |
11 |
7,9 |
| 8,1 – 8,5 |
10 |
8,3 |
| 8,5 – 8,9 |
24 |
8,7 |
| 8,9 – 9,3 |
21 |
9,1 |
| 9,3 -9,7 |
21 |
9,5 |
| 9,7 – 10,1 |
11 |
9,9 |
| 10,1- 10,4 |
10 |
10,3 |
| 10,4 – 10,8 |
3 |
10,6 |
| 10,8 -11,2 |
3 |
11 |
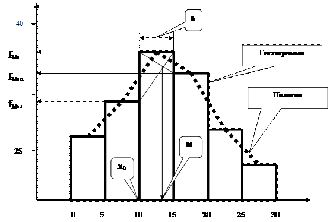
На основании таблицы построена гистограмма, рис. 5.2.
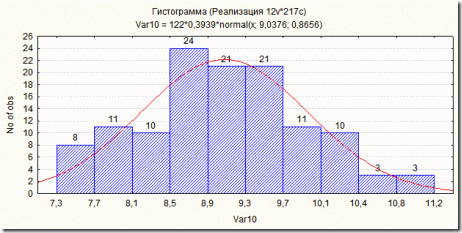
Рис. 5.2 Гистограмма распределения частот дневных выручек
Следует иметь ввиду, что самый быстрый способ преобразования временного ряда в частотный использования пакета Statistica. Для этого исходные данные копируются в пакет, а затем нажимая кнопку «Граф» в выпавшем меню выбирается оция «Гистограмма» и в ней определяется число групп («Категория» в нашем случае 10), «Тип графика» Обычный «Variables» (Данные) – соответствующий столбец с данными. OK. В построенной гистограмме можно поставить значение частот для этого при нахождении курсора гистограмме в меню вызванном правой клавишей выбирает опцию «Метки точки» кликнуть на окне «Показать метки»и кликнуть на окне «Счет».
Решение
Средне дневная реализация определяется x
ср=∑(x
i*f
i)/∑f
i = 1370/100=13,7 тыс.руб.
Мода (Мо) — значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту (частость).
В
дискретном ряду мода определяется визуально по максимальной частоте или частости.
В
интервальном ряду по наибольшей частоте определяется модальные интервал (например, по данным таблицы наибольшая частота f
max= 30 %, а модальный интервал Мо=10-15 тыс.руб.), а конкретное значение моды в модальном интервале определяется:
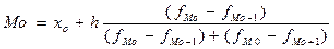
,
где
xoи
h –соответственно нижняя граница и величина модального интервала (например, по данным таблицы
xo=10 тыс.руб, а
h=(20-15)=5 тыс.руб., см. рис. 3.3);
fM0 – частота (частность) модального интервала (по данным таблицы
fM0 =30%,
fMo-1=19%
fMo+1=24% соответственно значение моды: Mo=10+5(30-19)/[(30-19)+(30-24)]=13.24 тыс.руб.).
Медиана (Ме) — значение признака (варианта), приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. это вариант, который делит ряд распределения на две равные по объему части.
Медиана, как и мода, не зависит от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределенными границами.
Для определения медианы в ранжированном ряду необходимо вначале найти номер медианы:
N=(n+1)/2 (в нашем случае N=(100+1)/2=50.5%, см. рис. 5.4). Затем по накопленным (кумулятивным) частотам
Si дискретного ряда определяется медиальный интервал (в нашем случае интервал совпадает с модальным интервалом (такое совпадение не всегда обязательно, но встречается часто) это 10 – 15 тыс.руб, поскольку ближайшая большая 50% накопленная частота
Si = 59%).
Рис. 5.3. Гистограмма и полигон
В
дискретном ряду распределения медианы находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае
интервального (вариационного) ряда распределения конкретного значение медианы вычисляется по формуле:
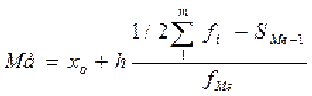
где
xoи
h –соответственно нижняя граница и величина медианного интервала (по данным таблицы
xo=10 тыс.руб., а
h=(15-10)=5 тыс.руб.);
fMe– частота (частность) медианного интервала (по данным таблицы
fMe=30%);
SMe-1 – накопленная частота предмедиального интервала (
SMe-1= 29%).
Значение медианы для примера из таблицы Ме=10+5(50-29)/30=13,5 тыс.руб. Откуда можно заключить, что половина всего оборудование имеет возраст не более 13,5 тыс.руб. или половина всего оборудования имеет возраст больше 13,5 тыс.руб.
В симметричных рядах распределение значения моды и медианы совпадают со вредней величиной
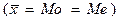
, а в умеренно асимметричных рядах они соотносятся:
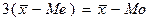
.
Кроме медианы в анализе закономерностей распределения используются также квартели и децели, при расчете которых в формуле расчета медиального значения
Ме множитель ½ заменяется на 0,25 и 0,1 соответственно.
Показатели степени вариации и способы их расчета. Для измерения и оценки вариации используют абсолютные и относительные характеристики.
Наиболее поверхностная оценка рассеяния (вариации) совокупности распределения определяется с помощью
вариационного размаха R, который показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака:
R=xmax-xmin.
Рис. 5.4. Кумулята
Среднее линейное отклонение 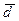
является обобщающей мерой вариации индивидуальных значений признака от средней арифметической величины. Она дает абсолютную меру вариации.
Для интервальных (вариационных) рядов взвешенная средняя определяется:
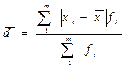
Для приведенного выше примера -
![clip_image025[1] clip_image025[1]](https://moscow-stud.com/wp-content/uploads/2013/05/1a3118043347_9996/clip_image0251_thumb.gif)
=531,6/100=5,32 тыс.руб.
Дисперсия (s)
2 — это средний квадрат отклонений индивидуальных значений признака от средней величины. Дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, а также для проверки статистических гипотез.
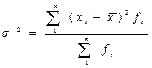
Для приведенного выше примера -
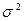
=4256/100=42,56.
Среднее квадратическое отклонение - s представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней, т.е. оно исчисляется путем извлечения квадратного корня из дисперсии и измеряется в тех же единицах, что и варьирующий признак.
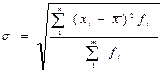
Для приведенного выше примера -
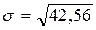
=6 тыс.руб.
Коэффициент осцилляции:
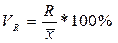
Для приведенного выше примера -
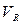
=182,48%.
Линейный коэффициент вариации:
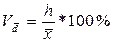
Для приведенного выше примера -
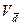
= 36,5%.
Коэффициент вариации:
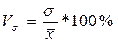
Для приведенного выше примера
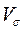
= 43,8 %.
Показатели асимметрии и эксцесса. Симметричным называется распределение у которого частоты равноотстоящие от моды равны между собой, следовательно выполняется соотношение
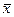
=Мо=Ме. Соответственно наиболее простой мерой асимметрии является (x
ср-Мо).
Коэффициент асимметрии Пирсона:
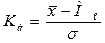
При К
а>0 скошенность ряда правосторонняя (т.е.
![clip_image049[1] clip_image049[1]](https://moscow-stud.com/wp-content/uploads/2013/05/1a3118043347_9996/clip_image0491_thumb.gif)
>Mo), при К
а<0 скошенность ряда левосторонняя (т.е.
![clip_image049[2] clip_image049[2]](https://moscow-stud.com/wp-content/uploads/2013/05/1a3118043347_9996/clip_image0492_thumb.gif)
<Mo). В нашем примере К
а=0,08 и следовательно ряд характеризуется правосторонней незначительной асимметрией.
Нормальный коэффициент асимметрии третьего порядка. Часто используется в прикладных расчетах. Коэффициент не зависит от масштаба, выбранного при измерении варианта, так как является отвлеченной величиной и определяется по формуле:
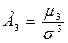
,
где
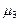
- центральный момент третьего порядка и определяется:
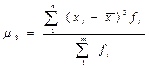
Для случая из таблицы 4 нормальный коэффициент асимметрии третьего порядка будет равен А
3=412,64/216 =1,91.
Нормальный коэффициент асимметрии четвертого порядка. Используется для определения «крутизны» («заостренности») графика распределения частот. Определяется по формуле:
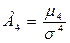
,
где
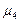
- центральный момент третьего порядка и определяется:
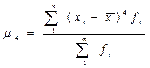
При нормальном распределении А
4=3. Для измерении асимметрии эталоном служит симметричное (нормальное) распределение, для которого А
3=0.
Для случая из таблицы 4 нормальный коэффициент асимметрии четвертого порядка будет равен А
4=3,42.
Показатель эксцесса распределения:
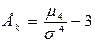
.
При Е
k>0 распределение островершинное, при Е
k <0 – плосковершинное.
В нашем примере Е
k=(3,42-3)=0,42 и следовательно ряд островершинный.
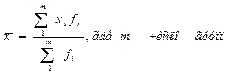 · на основе частостей
· на основе частостей
 Рис. 5.1 Динамика продаж услуги, тыс.руб.
В результате исходные данные преобразуются в частотный вид см. табл. 5.3.
Таблица 5.3
Частотная интерпретация исходных данных
Рис. 5.1 Динамика продаж услуги, тыс.руб.
В результате исходные данные преобразуются в частотный вид см. табл. 5.3.
Таблица 5.3
Частотная интерпретация исходных данных
 Рис. 5.2 Гистограмма распределения частот дневных выручек
Следует иметь ввиду, что самый быстрый способ преобразования временного ряда в частотный использования пакета Statistica. Для этого исходные данные копируются в пакет, а затем нажимая кнопку «Граф» в выпавшем меню выбирается оция «Гистограмма» и в ней определяется число групп («Категория» в нашем случае 10), «Тип графика» Обычный «Variables» (Данные) – соответствующий столбец с данными. OK. В построенной гистограмме можно поставить значение частот для этого при нахождении курсора гистограмме в меню вызванном правой клавишей выбирает опцию «Метки точки» кликнуть на окне «Показать метки»и кликнуть на окне «Счет».
Решение
Средне дневная реализация определяется xср=∑(xi*fi)/∑fi = 1370/100=13,7 тыс.руб.
Мода (Мо) — значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту (частость).
В дискретном ряду мода определяется визуально по максимальной частоте или частости.
В интервальном ряду по наибольшей частоте определяется модальные интервал (например, по данным таблицы наибольшая частота fmax= 30 %, а модальный интервал Мо=10-15 тыс.руб.), а конкретное значение моды в модальном интервале определяется:
Рис. 5.2 Гистограмма распределения частот дневных выручек
Следует иметь ввиду, что самый быстрый способ преобразования временного ряда в частотный использования пакета Statistica. Для этого исходные данные копируются в пакет, а затем нажимая кнопку «Граф» в выпавшем меню выбирается оция «Гистограмма» и в ней определяется число групп («Категория» в нашем случае 10), «Тип графика» Обычный «Variables» (Данные) – соответствующий столбец с данными. OK. В построенной гистограмме можно поставить значение частот для этого при нахождении курсора гистограмме в меню вызванном правой клавишей выбирает опцию «Метки точки» кликнуть на окне «Показать метки»и кликнуть на окне «Счет».
Решение
Средне дневная реализация определяется xср=∑(xi*fi)/∑fi = 1370/100=13,7 тыс.руб.
Мода (Мо) — значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту (частость).
В дискретном ряду мода определяется визуально по максимальной частоте или частости.
В интервальном ряду по наибольшей частоте определяется модальные интервал (например, по данным таблицы наибольшая частота fmax= 30 %, а модальный интервал Мо=10-15 тыс.руб.), а конкретное значение моды в модальном интервале определяется:
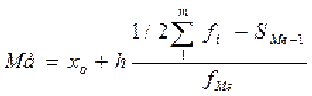 где xoиh –соответственно нижняя граница и величина медианного интервала (по данным таблицы xo=10 тыс.руб., аh=(15-10)=5 тыс.руб.);
fMe– частота (частность) медианного интервала (по данным таблицы fMe=30%);
SMe-1 – накопленная частота предмедиального интервала (SMe-1= 29%).
Значение медианы для примера из таблицы Ме=10+5(50-29)/30=13,5 тыс.руб. Откуда можно заключить, что половина всего оборудование имеет возраст не более 13,5 тыс.руб. или половина всего оборудования имеет возраст больше 13,5 тыс.руб.
В симметричных рядах распределение значения моды и медианы совпадают со вредней величиной
где xoиh –соответственно нижняя граница и величина медианного интервала (по данным таблицы xo=10 тыс.руб., аh=(15-10)=5 тыс.руб.);
fMe– частота (частность) медианного интервала (по данным таблицы fMe=30%);
SMe-1 – накопленная частота предмедиального интервала (SMe-1= 29%).
Значение медианы для примера из таблицы Ме=10+5(50-29)/30=13,5 тыс.руб. Откуда можно заключить, что половина всего оборудование имеет возраст не более 13,5 тыс.руб. или половина всего оборудования имеет возраст больше 13,5 тыс.руб.
В симметричных рядах распределение значения моды и медианы совпадают со вредней величиной 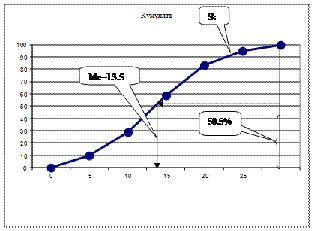
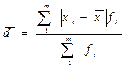 Для приведенного выше примера -
Для приведенного выше примера - 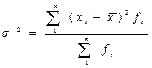 Для приведенного выше примера -
Для приведенного выше примера - 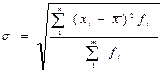 Для приведенного выше примера -
Для приведенного выше примера - 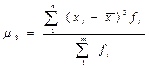 Для случая из таблицы 4 нормальный коэффициент асимметрии третьего порядка будет равен А3=412,64/216 =1,91.
Нормальный коэффициент асимметрии четвертого порядка. Используется для определения «крутизны» («заостренности») графика распределения частот. Определяется по формуле:
Для случая из таблицы 4 нормальный коэффициент асимметрии третьего порядка будет равен А3=412,64/216 =1,91.
Нормальный коэффициент асимметрии четвертого порядка. Используется для определения «крутизны» («заостренности») графика распределения частот. Определяется по формуле:
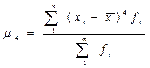 При нормальном распределении А4=3. Для измерении асимметрии эталоном служит симметричное (нормальное) распределение, для которого А3=0.
Для случая из таблицы 4 нормальный коэффициент асимметрии четвертого порядка будет равен А4=3,42.
Показатель эксцесса распределения:
При нормальном распределении А4=3. Для измерении асимметрии эталоном служит симметричное (нормальное) распределение, для которого А3=0.
Для случая из таблицы 4 нормальный коэффициент асимметрии четвертого порядка будет равен А4=3,42.
Показатель эксцесса распределения:
