1. Главная
2. Полезные советы
3. Теорема Гаусса-Маркова

Теорема Гаусса-Маркова

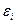
Для того, чтобы регрессионный анализ, основанный на методе наименьших квадратов (МНК), давал наилучшие из всех возможных результаты, должны выполняться условия Гаусса-Маркова, при выполнении которых модель называется классической нормальной линейной регрессионной моделью. Наряду с условиями Гаусса-Маркова обычно предполагается, что случайный член имеет нормальное распределение. При этом требование некоррелированности значений случайного члена эквивалентно их независимости. Если условия Гаусса-Маркова выполняются, то оценки, сделанные с помощью МНК, являются наилучшими оценками. Они обладают свойствами: - несмещенности - это означает отсутствие систематической ошибки в положении линии регрессии; - эффективности – имеют наименьшую дисперсию в классе всех линейных несмещенных оценок; - состоятельности – при достаточно большом объеме данных оценки приближаются к истинным значениям. Первое условие Гаусса-Маркова означает, что случайный член не должен иметь систематического смещения. Если постоянный член включен в уравнение регрессии, то это условие выполняется автоматически. Второе условие означает, что дисперсия случайного члена в каждом наблюдении имеет только одно значение. Но ее величина заранее неизвестна, и одна из задач регрессионного анализа состоит в ее оценке. Условие независимости дисперсии случайного члена от номера наблюдения называется гомоскедастичностью. Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью. Характерная диаграмма рассеяния для одного из возможных вариантов гетероскедастичности представлена на рис. 3.1. Если условие гомоскедастичности не выполняется, то оценки коэффициентов регрессии будут неэффективными, хотя и несмещенными. Существуют специальные методы диагностирования и устранения гетероскедастичности. 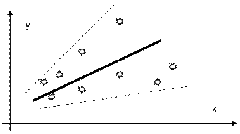Рис. 3.1. Случай гетероскедастичности остатков Третье условие указывает на некоррелированность случайных членов для разных наблюдений. Это условие часто нарушается, когда данные являются временными рядами. В случае когда третье условие не выполняется говорят об автокорреляции остатков. Если условие независимости случайных членов не выполняется, то оценки коэффициентов регрессии, полученные по МНК, оказываются неэффективными, хотя и несмещенными. Существуют методы диагностирования и устранения автокорреляции остатков. Четвертое условие. Если условие неслучайности, объясняющей переменной не выполняется, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными. Мерой отклонения зависимой переменной от значений, предсказываемых уравнением регрессии, служит остаточная дисперсия. 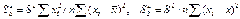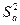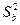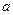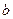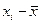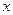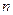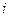Дисперсия коэффициентов регрессии определяется следующим образом: , где и – дисперсия коэффициентов и уравнения регрессии; – i-ое и среднее значения объясняющей переменной ; – число пар переменных в выборке; – порядковый номер пары переменных в выборке. Величины и - стандартные ошибки коэффициентов регрессии. Если испытываете трудности в написании курсовой работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.