-
Главная
-
Полезные советы
-
Теорема Гюйгенса. Скорость и ускорение точки в криволинейном движении.
Теорема Гюйгенса. Скорость и ускорение точки в криволинейном движении.
Формула
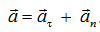
выражает теорему Гюйгенса: ускорение точки при криволинейном движении равно геометрической сумме касательного и нормального ускорений. Из (1.13) следует, что проекция ускорения точки на бинормаль всегда равна нулю:
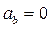
.
Вектор касательного ускорения
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/1fc137b08a0d_D635/clip_image0024_thumb.gif)
направлен в точке М по касательной к траектории в соответствии со знаком
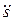
(аналогично вектору скорости
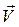
). Вектор нормального ускорения
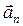
направлен вдоль главной нормали к центру кривизны траектории (рис. 1.4).
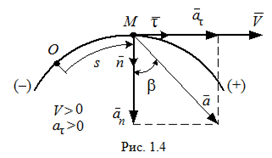
Поскольку векторы
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/1fc137b08a0d_D635/clip_image0026_thumb.gif)
и
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/1fc137b08a0d_D635/clip_image0044_thumb.gif)
взаимно перпендикулярны, то вектор ускорения
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/1fc137b08a0d_D635/clip_image0064_thumb.gif)
точки М изобразим диагональю прямоугольника, построенного на составляющих
![clip_image002[7] clip_image002[7]](https://moscow-stud.com/wp-content/uploads/1fc137b08a0d_D635/clip_image0027_thumb.gif)
и
![clip_image004[5] clip_image004[5]](https://moscow-stud.com/wp-content/uploads/1fc137b08a0d_D635/clip_image0045_thumb.gif)
как на сторонах. Его модуль и направление определяются по формулам
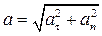
; (1.16)
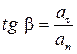
. (1.17)
Если знаки
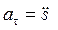
и
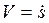
в данный момент времени одинаковые (оба положительные (рис. 1.4) или отрицательные), то точка движется ускоренно, а если знаки противоположные - замедленно.
Если испытываете трудности в написании
курсовой работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
 Поскольку векторы
Поскольку векторы 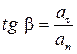 . (1.17)
Если знаки
. (1.17)
Если знаки  Поскольку векторы
Поскольку векторы 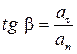 . (1.17)
Если знаки
. (1.17)
Если знаки