-
Главная
-
Полезные советы
-
Уравнения движения точки в декартовых координатах.
Уравнения движения точки в декартовых координатах.
Уравнение
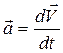
называется уравнением движения точки в декартовых координатах. Уравнение траектории точки можно определить исключением времени t как параметра из уравнений (1.3).
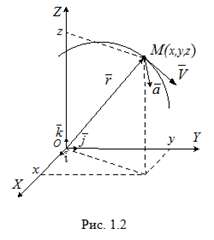
Учитывая связь
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image0024_thumb.gif)
,
(
![clip_image002[6] clip_image002[6]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image0026_thumb.gif)
- единичные орты декартовых осей OX, OY, OZ на рис. 1.2), определения (1.2) и (1.3), найдем скорость и ускорение точки в декартовых координатах:
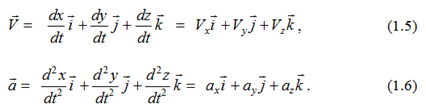
Из (1.5) и (1.6) следует, что
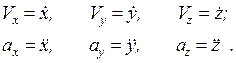
(1.7)
Проекции вектора скорости точки на декартовые оси равны первым производным, а проекции вектора ускорения - вторым производным от соответствующих координат по времени. В (1.7) и далее производная по времени обозначается точкой, стоящей над величиной
![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image00210_thumb.gif)
.
Скорость и ускорение точки по величине определяется по формулам:
![clip_image004[5] clip_image004[5]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image0045_thumb.gif)
(1.8)
Направление векторов
![clip_image006[5] clip_image006[5]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image0065_thumb.gif)
и
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image0084_thumb.gif)
найдем с помощью косинусов направляющих углов с осями OX, OY, OZ:
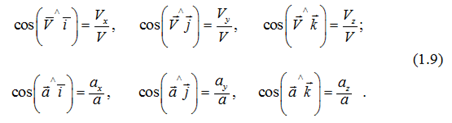
Если испытываете трудности в написании
контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
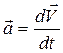 называется уравнением движения точки в декартовых координатах. Уравнение траектории точки можно определить исключением времени t как параметра из уравнений (1.3).
называется уравнением движения точки в декартовых координатах. Уравнение траектории точки можно определить исключением времени t как параметра из уравнений (1.3).
 Учитывая связь
Учитывая связь 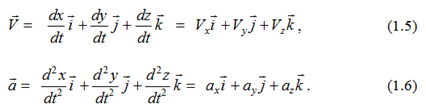 Из (1.5) и (1.6) следует, что
Из (1.5) и (1.6) следует, что
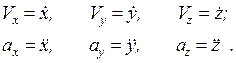 (1.7)
Проекции вектора скорости точки на декартовые оси равны первым производным, а проекции вектора ускорения - вторым производным от соответствующих координат по времени. В (1.7) и далее производная по времени обозначается точкой, стоящей над величиной
(1.7)
Проекции вектора скорости точки на декартовые оси равны первым производным, а проекции вектора ускорения - вторым производным от соответствующих координат по времени. В (1.7) и далее производная по времени обозначается точкой, стоящей над величиной ![clip_image002[10] clip_image002[10]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image00210_thumb.gif) .
Скорость и ускорение точки по величине определяется по формулам:
.
Скорость и ускорение точки по величине определяется по формулам:
![clip_image004[5] clip_image004[5]](https://moscow-stud.com/wp-content/uploads/ba6a5b3990e8_D515/clip_image0045_thumb.gif) (1.8)
Направление векторов
(1.8)
Направление векторов 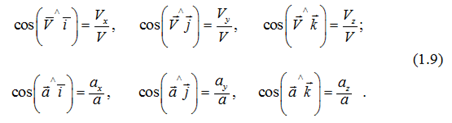 Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
