-
Главная
-
Полезные советы
-
Устранение автокорреляции. Поправка Прайса-Уинстена.
Устранение автокорреляции. Поправка Прайса-Уинстена.
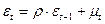 (1)
(1)
Наиболее лучший способ устранения – это определить фактор, который вызывает автокорреляцию остатков и включает его в уравнение регрессии, но это трудно сделать, так как:
- нам неизвестен фактор
- этот фактор трудно измерить
Поэтому используют другие способы. Пусть закономерность, описывающая автокорреляцию и нам известно
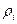
. Для простоты рассмотрим уравнение 1-го порядка:
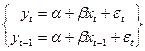
(
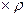
) (2)
Получим 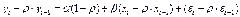
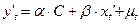
(3), следовательно полностью устранена автокорреляция.
При использовании такого подхода пропадает первое наблюдение. Если выборка маленькая, то потеря 1-го наблюдения может снизить эффективность оценок, вызванную автокорреляцией остатков.
Для возвращения 1-го наблюдения используется следующий подход. Если уравнение (3) имеет случайную составляющую, не связанную с другими случайными остатками в наблюдениях 2,3,4…n, то эти случайные составляющие не коррелируют и с 1-ым остатком, т.е.
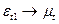
, а значит мы можем использовать 1-ое наблюдение без преобразований:
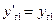
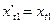

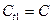
. Однако в этом случае уравнение (1) будет оказывать, при применении МНК, неоправданно большое влияние на определенные оценки параметров.
Для устранения этого дисбаланса между уравнениями Прайс и Уинстен предложили умножить 1-ое уравнение на поправочный коэффициент
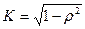
. В этом случае уравнение становится соизмеримым с другими уравнениями.
Метод Кокрана-Оркатта
Данный метод используется для устранения автокорреляции итерационную процедуру, которую можно представить в виде следующих этапов:
- оцениваем исходное регрессионное уравнение, то есть находим λ и β.
![clip_image002[16] clip_image002[16]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image00216_thumb.gif)
- вычисляем остатки
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image0044_thumb.gif)
- находим оценку ρ коэффициента автокорреляции (1)
- используя данную оценку ρ находим уравнение (3)
- производим определение параметров уравнения (3) и находим новые значения оценок λ и β
- повторно вычисляем остатки
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image0064_thumb.gif) и фактически возвращаемся к этому №3
и фактически возвращаемся к этому №3
Процесс повторяется до тех пор, пока не будет получена требуемая точность сходимости в оценках λ и β
Метод Хилдрета–Лу
В данном методе исследователь задает интервал изменения величины
ρ, допустим в пределах
![clip_image008[4] clip_image008[4]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image0084_thumb.gif)
Для каждого значения
ρ производится оценка параметров λ и β из уравнения (3). Затем из полученных результатов выбирается такой, который дает минимальную стандартную ошибку для преобразованного уравнения. Используемые в этом уравнении значения
ρ, λ и β принимаются за искомые.
В случае, когда статистика Дарбина–Уотсона указ.на очень тесную положительную автокорреляцию, можно использовать упрощенную процедуру, в которой принимается
ρ=1. В этом случае уравнение (3) принимает следующий вид:
![clip_image010[4] clip_image010[4]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image0104_thumb.gif)
Если испытываете трудности в написании
контрольной работы по эконометрике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
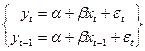 (
(![]()
![clip_image002[16] clip_image002[16]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image00216_thumb.gif)
![clip_image004[4] clip_image004[4]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image0044_thumb.gif)
![clip_image006[4] clip_image006[4]](https://moscow-stud.com/wp-content/uploads/8d2113fac85e_B6F1/clip_image0064_thumb.gif) и фактически возвращаемся к этому №3
и фактически возвращаемся к этому №3