1. Главная
2. Полезные советы
3. В условиях задачи 11 найти наивероятнейшее число удачных опытов и вероятность его появления.

В условиях задачи 11 найти наивероятнейшее число удачных опытов и вероятность его появления.

В условиях задачи 11 найти наивероятнейшее число удачных опытов и вероятность его появления.

(Задача 11. Вероятность получения удачного результата при проведении сложного химического опыта равна 3/4. Найти вероятность 6 удачных результатов в 10-ти опытах).

Решение:

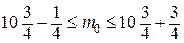
Число m₀ называется наивероятнейшим в n независимых испытаниях, если вероятность наступления события А при этом числе наибольшая. n·p – q ≤ m₀ ≤ n·p + p По условию задачи 11 вероятность проведения удачного опыта равна p = 3/4, значит вероятность неудачного опыта равна q = 1/4. Количество опытов равно п = 10. Составим неравенство 7,25 ≤ m₀ ≤ 8,25 Þ m₀ = 8 Наивероятнейшее число удачных опытов равно 8. 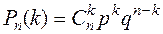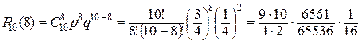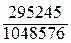Поскольку количество испытаний невелико (n = 10), то для нахождения вероятности того, что событие А появится точно k = 8 раз воспользуемся формулой Бернулли: , где q = 1 – p = » 0,282. Если испытываете трудности в написании контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.