-
Главная
-
Полезные советы
-
В условиях задачи 8 найти вероятность наивероятнейшего числа дней без дождя.
В условиях задачи 8 найти вероятность наивероятнейшего числа дней без дождя.
В условиях задачи 8 найти вероятность наивероятнейшего числа дней без дождя.
(Задача 8. С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из наугад взятых в этом месяце 8-ми дней 3 будут дождливыми?)
Решение:
Число m
0 называется наивероятнейшим в n независимых испытаниях, если вероятность наступления события А при этом числе наибольшая.
n·p – q ≤ m
0 ≤ n·p + p
По условию задачи 8 вероятность дня без дождя равна p = 9/15, значит вероятность дождливого дня равна q = 6/15. Составим неравенство
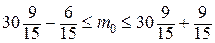
17,6 ≤ m
0 ≤ 18,6 Þ m
0 = 18
Наивероятнейшее число дней без дождя равно 18. Поскольку количество испытаний велико (n = 30) и нет возможности применить формулу Бернулли, то для нахождения вероятности наивероятнейшего числа дней без дождя воспользуемся локальной теоремой Лапласа:
![clip_image002[4] clip_image002[4]](https://moscow-stud.com/wp-content/uploads/8_A3A4/clip_image0024_thumb.gif)
и j(х) – диф. функция Лапласа-Гаусса
Определим аргумент функции Лапласа-Гаусса х:
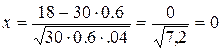
.
По таблице значений функции Гаусса определяем, что j(0) = 0,3989. Теперь
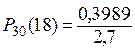
» 0,15.
Если испытываете трудности в написании
контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
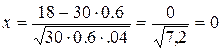 .
По таблице значений функции Гаусса определяем, что j(0) = 0,3989. Теперь
.
По таблице значений функции Гаусса определяем, что j(0) = 0,3989. Теперь
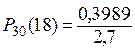 » 0,15.
Если испытываете трудности в написании контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
» 0,15.
Если испытываете трудности в написании контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена - от 99 рублей.
